Яков Перельман - Живой учебник геометрии

AB/CD=BE/DE, откуда AB=CD BE/DE

так как длины CD, BE и DE можно измерить, то нетрудно вычислить искомую ширину ( АВ ) озера.

78. Диаметр Солнца больше диаметра Земли в 109 раз; расстояние от Земли до Солнца 150 000 000 километров. Определить длину тени, отбрасываемой земным шаром (черт. 198).

Р е ш е н и е. Из подобия треугольников АОЕ и СРЕ (почему они подобны?) имеем

PE/OE = PC/OC

РЕ – есть искомая длина х тени; DE = OP + РЕ = 150 000 000 км + x; PC – радиус Земли; ОА – радиус Солнца. Мы знаем, что радиус Солнца в 109 раз больше радиуса Земли. Подставив эти величины в пропорцию, имеем

X/150 000 000 = 1/109

или 109 х = 150 000 000 + x , откуда

x = 150 000 000/109 = около 1 400 000 км.

На практике приходится нередко отыскивать отрезок такой длины, чтобы вместе с тремя данными отрезками могла быть составлена пропорция. Пусть, например, даны три отрезка а, b и с (черт. 199) и требуется отыскать четвертый отрезок х такой длины, чтобы возможна была пропорция:

а: b = с: х.

Задача эта решается так. На прямой линии (черт. 200) откладывают от точки М отрезки а и b . Под произвольным углом к а от точки М проводят прямую, на которой откладывают отрезок с. Концы N и Р отрезков а и с соединяют прямой и через конец Q отрезка b проводят QR параллельно NP. Отрезок MR и есть четвертая пропорциональная х , потому что

а: b = с: х.

Решение подобных задач называется «построением 4-й пропорциональной».

а: b = с: х.

Повторительные вопросы

Что значит: «построить 4-ую пропорциональную»? – Какие вы знаете способы ее построения?

Применения

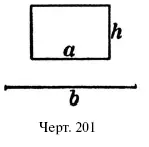
79. Прямоугольник со сторонами а и h (черт. 201) превратить в равновеликий прямоугольник с основанием b.

Р е ш е н и е. Надо начертить прямоугольник с основанием b и такой высотой х , чтобы bх = ax

Из последнего равенства вытекает пропорция b/a = h/x.

Следовательно, искомая высота х есть 4-я пропорциональная к a, h и b. Построив; ее по указанному раньше способу, мы сможем начертить и искомый прямо угольник.

80. Начертить прямоугольник с высотою b , равновеликий треугольнику с основанием а и высотою h .

Р е ш е н и е сводится к нахождению основания прямоугольника такой длины x , чтобы bх = bx = ah/2 ., т. е.,

чтобы x: a/2 = h: b

Значит, отрезок х есть 4-я пропорциональная к,a/2.h и b

81. Средняя линия трапеции p , высота – q. Построить равновеликий ей прямоугольник со стороною b.

Р е ш е н и е. Прямоугольник легко можно построить, если найдена будет его другая сторона х такой длины, что bx = pq , и следовательно х : р = д : b . Значит, х есть 4-я пропорциональная к р, q и b .

На свойстве подобных треугольников основано устройство так называемого «поперечного масштаба», которым пользуются при черчении планов. Устройство его показано на черт. 202. Пусть расстояние BA соответствует на плане в каком-нибудь определенном масштабе, 1 километру (или 5, 10, 20 километрам) в натуре. Это расстояние разделено на 10.равных частей; на столько же частей разделено» и расстояние KL = АВ; АК перпендикулярно к АВ и к КL ; точки деления АВ и КL соединены между собою наклонными линиями, как показано на чертеже. После сказанного в § 57 понятно, что отрезки параллельных прямых, отсекаемых: углом OLB составляют последовательно (считая от вершины L) 0,1, 0,2, 0,3, 0,4 и т. д. отрезка ОВ . А так как отрезок ОB сам составляет 0,1 длины АВ , то указанные отрезки составляют 0,01, 0,2, 0,03 и т. д. длины АВ .

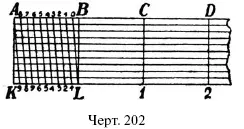
Отсюда ясна возможность помощью поперечного масштаба получать весьма малые доли масштабной единицы АВ . Если необходимо, например, раздвинуть ножки циркуля на 2,73 АВ , то помещают одну ножку циркуля на пересечении 2-й поперечной линии масштаба и 3-й (снизу) продольной; другую же – на пересечении той же 3-й продольной линии и 7-й косой: тогда острия циркуля окажутся раздвинутыми на 2,73 АВ . Чтобы раздвинуть их на 36.8 АВ , надо одно острие поместить на пересечении 3-й поперечной и 8-й продольной линии, а другое – на пересечении 8-й продольной и 6-й косой, и т. д.