Яков Перельман - Живой учебник геометрии

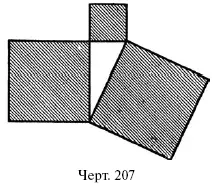
Соотношение это существует, как легко понять, также между площадями кругов, построенных на сторонах прямоугольного треугольника.

90. Начертить круг, площадь которого равна сумме площадей двух данных; кругов.

Р е ш е н и е. Радиус искомого круга должен быть такой длины х , чтобы ? x 2= xR 2+ ? r 2, где R и r – радиусы данных кругов. Сократив это уравнение на имеем: x 2= R 2+ r 2. Отсюда ясно, что искомый радиус есть гипотенуза треугольника, катеты которого r и R .

1) Устанавливая в предыдущем параграфе зависимость между сторонами прямоугольного треугольника, мы попутно вывели, что (черт. 206)

a2= bq,

c2= bp.

Выражая это соотношение словесно, мы скажем, что

к в а д р а т к а ж д о г о к а т е т а р а в е н п р о и з в е д е н и ю и з г и п о т е н у з ы и п р о е к ц и и э т о г о к а т е т а н а г и п о т е н у з у.

2) Кроме того, из подобия треугольников I и II следует, что

р : h= h: q , где h – высота,

т. е. h (высота) есть повторяющийся член непрерывной пропорции, другие члены которой есть р и q . Повторяющийся член непрерывной кратной пропорции принято называть средне-пропорциональным (или средне-геометрическим) между двумя остальными членами. Поэтому сейчас установленную зависимость можно высказать так:

в ы с о т а, п р о в е д е н н а я к г и п о т е н у з е, е с т ь с р е д н е – п р о п о р ц и о н а л ь н а я м е ж д у о т р е з к а м и г и п о т е н у з ы. Далее, из пропорции р : h = h: q следует, что h2 = pq , т. е.

к в а д р а т в ы с о т ы, п р о в е д е н н о й к г и п о т е н у з е, р а в е н п р о и з в е д е н и ю о т р е з к о в г и п о т е н у з ы.

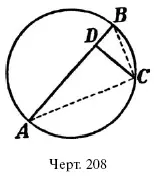
Проведем через: какую-нибудь точку окружности (черт. 208) перпендикуляр CD к диаметру АВ . Легко видеть, это этот перпендикуляр есть высота, проведенная к гипотенузе треугольника АСВ , так как угол АСВ – прямой (почему?). Поэтому

AD: DC = DC: DB,

или (DC)2= AD: DB;

другими словами:

п е р п е н д и к у л я р, п р о в е д е н н ы й и з к а к о й – н и б у д ь т о ч к и о к р у ж н о с т и к д и а м е т р у, е с т ь с р е д н е – п р о п о р ц и он а л ь н о е м е ж д у о т р е з к а м и д и а м е т р а. Этим свойством можно пользоваться, между прочим, в тех случаях, когда требуется построить к двум данным отрезкам средне-пропорциональный. Если данные отрезки а и l и требуется найти отрезок х такой длины, чтобы

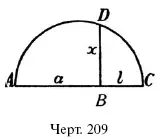
а : х = х : l ,

то откладывают рядом а и l (черт. 209), строят на АС , как на диаметре, полуокружность и из точки В восставляют перпендикуляр до пересечения с окружностью в точке D : отрезок BD = x .

Повторительные вопросы к §§ 71–73

Какое вы знаете соотношение между катетами и гипотенузой? – Между гипотенузой, катетом и его проекцией на гипотенузу? – Между высотой, проведенной к гипотенузе, и отрезком гипотенузы? – Между перпендикуляром, проведенным из точки окружности к диаметру и отрезками диаметра? – Что значит: найти? средне-пропорциональное между двумя отрезками? Как это сделать?

Применения

91. Чтобы определить расстояние от точки В (черт. 210) до недоступной точки A провешивают прямую BN под прямым углом к направлению АВ и из произвольной точки С этой прямой провешивают CD перпендикулярно к направлению AC ? Как, пользуясь этим построением, определить искомое расстояние АВ ?

Р е ш е н и е. Надо измерить расстояния ВС и ВD . Расстояние АВ оп-редется из равенства:

(BC)2= AB?BD,

откуда

AB = (BC)2/ BD

92. Начертить квадрат, равновеликий данному треугольнику с основанием а высотою h .

Р е ш е н и е. Задача сводится к отысканию стороны квадрата такой длины х , чтобы x2 = ? ah , т. е., чтобы a/2: х = х : h .

Отсюда видно, что искомый отрезок средне-пропорциональное между a/2 и h .

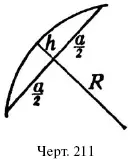
93. Найти стрелку h дуги (черт. 211) радиуса R , если длина стягивающей хорды = a .