Яков Перельман - Живой учебник геометрии

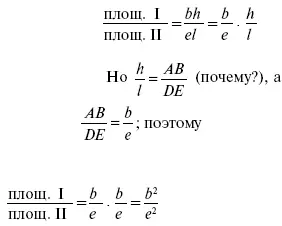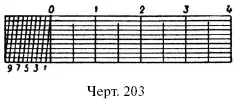
На черт. 203 изображен поперечный масштаб, дающий возможность откладывать отрезки с точностью до 0,1 миллиметра.

На подобии фигур основано также устройство и употребление прибора, называемого п а н т о г р а ф о м и служащего для перерисовывания фигур в измененном масштабе. Он состоит (черт. 204) из четырех планок АВ, BC, CD и AD , соединенных в форме параллелограмма так, что планки могут свободно вращаться в углах; поперечная планка ЕF располагается параллельно AD и может быть перемещаема по желанию. При употреблении прибора его укрепляют неподвижно в А и обводят перерисовываемый контур штифтом K ; тогда карандаш С вычерчивает тот же контур в увеличенном виде; все размеры получаются в столько раз крупнее, во сколько раз АС больше АК (или АВ больше АЕ ). Если, например, штифт А (черт. 204) переместился в N , т. е. прошел черту KN , то карандаш С переместился в М , т. е. начертил линию СМ ; из подобия треугольников АСМ и AKN (почему они подобны?) имеем, что СМ : KN – АС : АК , или АВ : АЕ . Отсюда следует, что желая увеличить рисунок, например, в 5 раз, мы должны поместить планку EF так, чтобы АВ было в 5 раз больше АЕ.

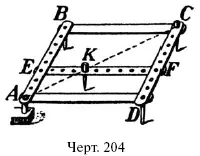
Нетрудно догадаться, как следует пользоваться пантографом для перерисовывания фигур и в у м е н ь ш е н н о м масштабе.

Предварительное упражнение

В треугольниках АВС и DEF уг. A = уг. D: ВМ и EN – высоты. Укажите все подобные треугольники в этих фигурах.

Между площадями подобных треугольников существует определенное соотношение, которое мы сейчас установим.

Пусть у нас имеются два подобных треугольника I и II (черт. 205). Проведем высоты ВМ = h и EN = l к сходственным сторонам АС = b и DF = e . Площадь треугольника I равна bh , треугольника II – el . Отношение их равно

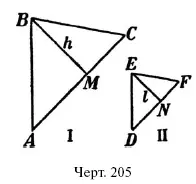
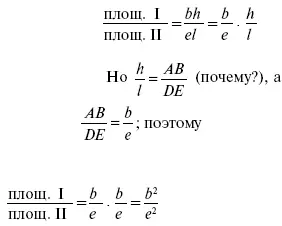
Значит,

п л о щ а д и п о д о б н ы х т р е у г о л ь н и к о в о т н о с я т с я к а к к в а д р а т ы с х о д с т в е н н ы х с т о р о н.

То, что мы установили в предыдущем параграфе для подобных треугольников, справедливо, как сейчас увидим; и для всяких подобных многоугольников: их площади относятся, как квадраты сходственных сторон. Вообще,

п л о щ а д и в с я к и х п о д о б н ы х ф и г у р о т н о с я т с я м е ж д у с о б о ю к а к к в а д р а т ы и х л и н е й н ы х р а з м е р о в. Это вытекает из следующих соображений. Пусть у нас имеются две подобные фигуры, при чем линейные размеры первой фигуры в 10 раз меньше размеров второй фигуры. Покроем меньшую фигуру палеткой, разграфленной на миллиметровые квадратики, а большую фигуру – палеткой, разграфленной на сантиметровые квадратики. Так как все линейные размеры первой фигуры содержат столько миллиметров, сколько размеры второй фигуры содержат сантиметров, то первая фигура будет заключать столько же миллиметровых квадратиков, сколько вторая – сантиметровых. Число квадратиков в обеих фигурах одинаково, но каждый квадратик первой фигуры меньше квадратика второй фигуры. Значит, площадь первой фигуры меньше площади второй во столько раз, во сколько один миллиметровый квадратик меньше сантиметрового, т. е. в 10 ? 10 = 100 раз.

Если линейные размеры подобных фигур относятся не как 1: 10, а например, как 1: 7, то сходным рассуждением можно установить, что площадь первой фигуры меньше второй в 49 раз; при отношении линейных размеров 8: 3 – больше в 64/9 раз и т. п.

Поэтому, если план здания исполнен в масштабе 1/20,то каждый его участок меньше площади того же участка в натуре в 20 ? 20, т. е. в 400 раз.

Повторительные вопросы к §§ 68–70

Как относятся площади подобных треугольников? – Многоугольников? – Всяких вообще плоских «фигур? – Справедливо ли это правило для кругов?

Применения

82. С дуба сорвано два листа одинаковой формы, длиною один 12 см, другой 15 см. Во сколько раз площадь второго листа больше площади первого?