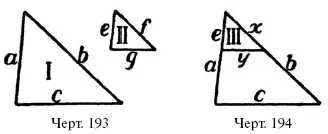Яков Перельман - Живой учебник геометрии

ED/ EM = 5/2 = EF/ EN

Но так как EF = AB , a EN = BC , то

ED/ AB = EF/ BC

Значит, стороны ЕD, AB, EF и BC – пропорциональны.

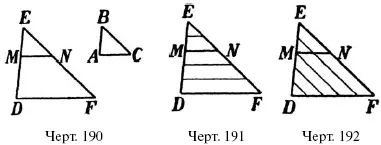
Для подобия треугольников необходимо еще, чтобы и отношение третьей пары сторон DF: AC равнялось отношению ED: АВ (или EF: BC ). Чтобы и в. этом удостовериться, проведем через точки деления стороны ED (черт. 192) ряд прямых, параллельных EF . Сторона MN разделится тогда на 2 равные части (почему?), a DF – на 5 таких же частей (почему?), и станет ясно, что

DE/AC=5/2=ED/AB=EF/BC

Итак, если углы одного треугольника равны углам другого, то стороны, прилегающие к равным углам (или лежащие против равных углов) пропорциональны.

П р и м е ч а н и е. Стороны треугольников могут иметь такую длину, что невозможно выполнить деление их, как указано было на черт. 191: ни одна точка деления не приходится в точке М. Однако, рассмотренное сейчас свойство сохраняется и в таком случае (это доказывается в более полных учебниках).

Мы сейчас доказали, что в двух треугольниках при равенстве, углов стороны должны быть пропорциональны. Покажем теперь, что и наоборот: при пропорциональности сторон треугольники имеют соответственно равные углы.

Это надо понимать так. Если длины сторон двух треугольников (напр. I и II на черт. 193) таковы, что

a/e = b/f = c/g

то угол против стороны a равен углу против стороны е , угол против b = углу против f , и угол против c = углу против g .

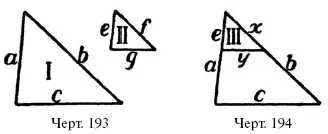
В этом легко убедиться, отложив (черт. 194) от вершины треугольника I на стороне а сторону е и проведя через конец ее прямую х , параллельную с . Она отсечет от треугольника I меньший треугольник III, стороны которого обозначим через е, х, у . Этот треугольник III имеет углы соответственно равные углам треугольника I. А мы сейчас доказали, что в таком случае

a/e=c/x=b/y

Нам известно, что a/e=b/f =c/g. Значит,

b/y=c/x=b/f=c/g

Но если

b/y=b/f

то y = f . А из равенства

c/x=c/g

следует, что x = g .

Другими словами: все стороны треугольника III равны сторонам треугольника II; а так как углы треугольника III равны углам треугольника I, то и углы треугольника II равны углам треугольника I. Это и требовалось доказать.

Повторительные вопросы к §§ 64 и 65

Как вы назовете фигуры, имеющие равные стороны и одинаковую форму? – Равные стороны и неодинаковую форму? Неравные стороны и одинаковую форму? – Какие стороны многоугольников называются сходственными? – Покажите, пользуясь чертежом, какие условия необходимы для подобия двух многоугольников. Покажите, пользуясь чертежом, какие соотношения существуют в двух подобных треугольниках. – Какие стороны подобных треугольников называются сходственными? А в каком случае стороны называются соответственными?

Применения

75. Найти высоту дерева, пользуясь его тенью.

Р е ш е н и е. Где-нибудь возле дерева воткнем отвесно шест MN (черт. 195). Так как лучи солнца параллельны, то уг. Р = уг. С ; кроме того, мы знаем, что уг. В и уг. N – прямые. Значит, треугольники ABC и MNP подобны и, следовательно,

AB/MN = BC/NP

откуда неизвестная высота дерева

AB = MN ? BC/NP

Высоту шеста МN и длину теней DС и NP легко измерить, и тогда вычисляют высоту АВ дерева.

76. В пасмурный день можно пользоваться для определения высоты дерева способом, изображенным на черт. 196. В чем он состоит?

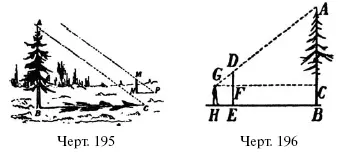
Р е ш е н и е. Наблюдатель помещает шест DE так, чтобы глядя на конец его D видеть его совпадающим с вершиной A . Измеряют DЕ, НЕ и НВ , кроме того, надо знать возвышение GН глаза G над почвой. Из подобия треугольников GАС и GDF имеем

AC/DF = DC/GF.

Дальнейшее – понятно без объяснений.

77. На черт. 197 изображен способ определения ширины АВ озера. Прямая CD провешивается параллельно АВ. Объясните, как найти искомую ширину ( АВ ) озера.

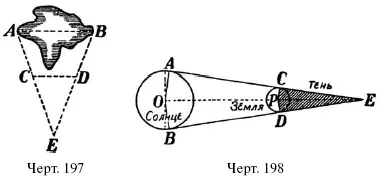
Р е ш е н и е. Из подобия треугольников ABE и СDE имеем