1 ...5 6 7 9 10 11 ...223 1.47.Найдите угол между двумя хордами, пересекающимися внутри окружности, если точка их пересечения удалена от центра окружности на 3 / 5ее радиуса и делит одну хорду пополам, а другую — в отношении 4 : 9.
1.48.Дан сектор ОАВ ( O — центр) с центральным углом в 90° и радиусом R . На отрезке ОВ , как на диаметре, построена полуокружность, лежащая внутри сектора. Найдите радиус окружности, касающейся этой полуокружности и отрезков ОА и AB .
1.49.В круге проведена хорда AB , пересекающая диаметр DE круга в точке M и наклоненная к нему под углом φ. Дано, что 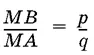 , где p и q — известные числа. Из точки В проведена хорда BC , перпендикулярная к диаметру DE , и точка С соединена с точкой А . Найдите площадь треугольника ABC , если радиус круга равен R .
, где p и q — известные числа. Из точки В проведена хорда BC , перпендикулярная к диаметру DE , и точка С соединена с точкой А . Найдите площадь треугольника ABC , если радиус круга равен R .
1.50.Площадь треугольника равна S , а длины его сторон образуют арифметическую прогрессию, разность которой равна d . Найдите радиус описанной окружности.
1.51.В треугольнике ABC точка P лежит на стороне AB и AB = 2 АР , точка Q — на стороне BC и BC = 4 BQ , точка R — на стороне AC и AC = 5 АВ . Отрезки PQ и BR пересекаются в точке T . В каком отношении точка T делит отрезок PQ ?
1.52.В треугольнике PQR на стороне PQ взята точка N а на стороне РR — точка L . Отрезки QL и RN пересекаются в точке T . Дано QN = RL , QT : TL = m : n . Найдите PN : PR .
1.53.Две окружности с центрами О 1и О 2пересекаются в точках M и N . Точка О 2лежит на первой окружности. Найдите периметр фигуры, являющейся пересечением данных окружностей, если 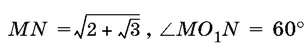 .
.
1.54.Найдите наибольшее возможное значение площади четырехугольника ABCD , если он вписан в окружность радиусом 1 и угол при вершине В меньше 45°.
Глава 2
Построения на плоскости
2.1.Пункты А и В находятся по разные стороны от реки, ширина которой постоянна, а берега прямолинейны. В каком месте надо возвести мост через реку, чтобы путь от одного пункта в другой был кратчайшим?
2.2.Постройте равносторонний треугольник ABC , если дана его сторона а и известно, что его стороны AB , AC и биссектриса AD (или их продолжения) проходят соответственно через три данные точки M , N , P , лежащие на одной прямой.
2.3.Постройте треугольник по стороне а , высоте h а и разности углов В − С = φ.
2.4.Постройте треугольник ABC по стороне b , радиусу R описанной окружности и медиане m с .
2.5.Постройте треугольник, зная центры его вписанной, описанной и вневписанной окружностей.
2.6.На сторонах AB и BC треугольника ABC или на их продолжениях постройте соответственно точки D и E так, чтобы AD = DE = EC .
2.7.Через точку, лежащую внутри угла, проведите прямую так, чтобы отсекаемый ею треугольник был наименьшей площади.
2.8.Постройте треугольник по А, h а и 2 p .
2.9.Внутри данного остроугольного треугольника ABC найдите точку P , сумма расстояний которой от вершин А , В и С была бы наименьшей.
2.10.Постройте прямоугольный треугольник по данной гипотенузе с и биссектрисе l прямого угла.
2.11.Постройте четырехугольник, если известны три его стороны и два внутренних острых угла, прилежащих к четвертой стороне.
2.12.Из данной точки M , лежащей вне круга, проведите секущую так, чтобы внешняя ее часть равнялась внутренней.
2.13.Через точку пересечения двух окружностей проведите секущую так, чтобы отрезок ее, заключенный внутри окружностей, имел данную длину а .
2.14.Через точку M внутри окружности проведите хорду так, чтобы разность ее отрезков равнялась данному отрезку.
2.15.Даны окружность, ее хорда CD и две точки А и В окружности, лежащие по одну сторону от CD . На этой окружности постройте точку M так, чтобы хорды AM и BM высекали на CD отрезок PQ заданной длины а .
Читать дальше
Конец ознакомительного отрывка
Купить книгу

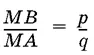 , где p и q — известные числа. Из точки В проведена хорда BC , перпендикулярная к диаметру DE , и точка С соединена с точкой А . Найдите площадь треугольника ABC , если радиус круга равен R .
, где p и q — известные числа. Из точки В проведена хорда BC , перпендикулярная к диаметру DE , и точка С соединена с точкой А . Найдите площадь треугольника ABC , если радиус круга равен R .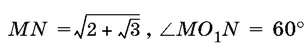 .
.










