Ответ . По определению параллельных прямых.
Пример 4.Почему сумма внутренних углов треугольника равна 180°?
Ответ . По теореме о сумме углов треугольника.
Пример 5.Почему сумма всех нечетных чисел, начиная с 1 до 2 n + 1, равна квадрату натурального числа n ?
Отвечая на этот вопрос, мы не можем сослаться на одну из теорем курса. Поэтому нужно приступить к доказательству. Вы найдете его в главе, посвященной математической индукции.
Глава 1
Геометрические задачи на плоскости
Обозначения: а, b, с — стороны треугольника; А, В, С — углы, лежащие против этих сторон, соответственно; m а — медиана стороны а ; l A — биссектриса угла А; h a — высота, опущенная на сторону а ; R — радиус описанной окружности; r — радиус вписанной окружности; P = 2р — периметр многоугольника.
Длиной биссектрисы внешнего угла А треугольника называется отрезок биссектрисы, заключенный между точкой А и точкой пересечения биссектрисы с продолжением стороны а .
Отношение площадей двух треугольников, имеющих общий угол, равно отношению произведений сторон, заключающих этот общий угол .
Имеет место формула, выражающая длину медианы треугольника через длины его сторон: 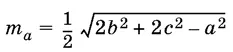 .
.
Если в многоугольник можно вписать окружность, то его площадь S = pr .
Площадь четырехугольника: S = ½ d 1 d 2sin α, где d 1и d 2— длины его диагоналей, а α — угол между ними.
При решении планиметрических задач приходится применять производные пропорции.
Если 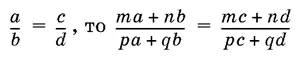 .
.
Если 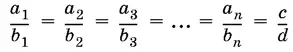 , то
, то
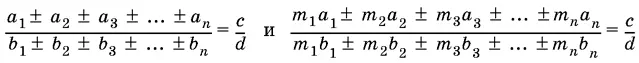 , где комбинация знаков берется любая, но одинаковая для числителя и знаменателя.
, где комбинация знаков берется любая, но одинаковая для числителя и знаменателя.
1.1.Вокруг правильного треугольника ABC описана окружность O радиусом R . Окружность O 1касается двух сторон AB и BC треугольника и окружности O . Найдите расстояние от центра окружности О 1до вершины А .
1.2.Высота равнобедренного треугольника с углом α при основании больше радиуса вписанного в него круга на m . Определите основание треугольника и радиус описанной окружности.
1.3.Докажите, что радиус окружности, делящей пополам стороны треугольника, вдвое меньше радиуса окружности, описанной около этого треугольника.
1.4.В треугольнике соединены основания биссектрис. Найдите отношение площади данного треугольника к площади образовавшегося треугольника, если стороны данного треугольника относятся как p : q : l .
1.5.Даны углы A, B, C треугольника ABC . Пусть окружность касается сторон BC , AC и AB треугольника соответственно в точках A 1, B 1, C 1. Найдите отношение площади треугольника A 1 B 1 C 1к площади треугольника ABC .
1.6.Дан треугольник ABC , углы B и C которого относятся как 3 : 1, а биссектриса угла А делит площадь треугольника в отношении 2 : 1. Найдите углы треугольника.
1.7.Найдите длину l биссектрисы внешнего угла А треугольника, если даны его стороны b и c и угол А между ними ( b ≠ c ).
1.8.В треугольнике площади S , с острым углом α при вершине А биссектриса угла А в p раз меньше радиуса описанного и в q раз больше радиуса вписанного круга. Найдите сторону треугольника, лежащую против угла А .
1.9.В треугольнике ABC проведены биссектрисы AM и BN. Пусть O — точка их пересечения. Известно, что
AO : OM = √3 : 1, а BO : ON = 1 : (√3 − 1).
Найдите углы треугольника.
1.10.Внутри угла а взята точка M . Ее проекции P и Q на стороны угла удалены от вершины O угла на расстояния OP = p и OQ = q . Найдите расстояния MP и MQ от точки M до сторон угла.
1.11.В остроугольном треугольнике две высоты равны 3 и 2√2 см, а их точка пересечения делит третью высоту в отношении 5 : 1, считая от вершины треугольника. Найдите площадь треугольника.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

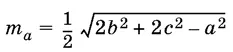 .
.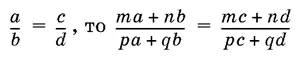 .
.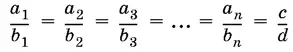 , то
, то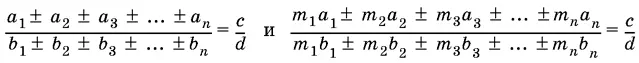 , где комбинация знаков берется любая, но одинаковая для числителя и знаменателя.
, где комбинация знаков берется любая, но одинаковая для числителя и знаменателя.










