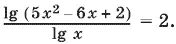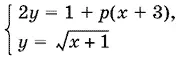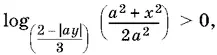Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

и укажите, при каких с ∈ R эта сумма принимает наибольшее значение.

5.Основанием треугольной пирамиды SABC служит треугольник АВС , y которого ВС = 1, СА = 13, а высота СЕ = √105. Каждое боковое ребро пирамиды образует с плоскостью АВС угол величиной α. Определите площадь основания и объем пирамиды.

1.Решите уравнение

2.Решите уравнение

|6 cos x − 1| = 4 cos 2 x + 3.

3.Решите неравенство

log 2(3 x − 5) + log ¼(2 x − 1) < 1.

4.В правильную четырехугольную пирамиду вписана сфера, которая касается основания и всех боковых граней. Сфера делит высоту пирамиды в отношении 1 : 3, считая от вершины. Найдите объем пирамиды, если апофема пирамиды равна а .

5.При а = 1 решите уравнение

(4 a + 2) sin x + 2 a cos 2 x + а + 1 = 0

и определите все значения а , при которых это уравнение имеет ровно одно решение, принадлежащее отрезку [0; 5π/ 6].

1.Из пункта А в пункт В одновременно вышли два пешехода. Когда первый прошел половину пути, второму осталось пройти 24 км, а когда второй прошел половину пути, первому осталось пройти 15 км. Найдите расстояние от пункта А до пункта В .

2.Найдите все корни уравнения

cos 2 x + cos 6 x = cos 4 x ,

принадлежащие промежутку [ π/ 2; π].

3.Решите уравнение

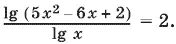
4.Решите неравенство 2 x + 1+ 3 < 2 1 − x .

5.Какая наибольшая площадь может быть y прямоугольного треугольника, одна вершина которого совпадает с точкой M (5; 0), другая лежит на графике функции y = x ³(5 − x ), 0 ≤ x ≤ 5, а вершина прямого угла — на оси Ox ?

6.Найдите все значения p , при которых система уравнений

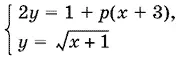
имеет единственное решение.

7.Основанием пирамиды ТАВС служит треугольник АВС с углом А , равным 60°. Боковое ребро ТА совпадает с высотой пирамиды и равно h ; ребро ТС перпендикулярно стороне основания ВС , а угол между ребром ТВ и биссектрисой основания АD равен 60°. Какую наименьшую площадь может иметь сечение пирамиды плоскостью, проходящей через биссектрису АD и пересекающую ребро ТВ ?

1.Решите уравнение

3 | x |= 5 x ² + 3 x .

2.Решите систему неравенств

3.В треугольнике АВС со стороной AB = √5 из вершины В к стороне AC проведены медиана ВМ = 2√2 и высота ВН = 2. Найдите сторону ВС , если известно, что ∠ АВС + ∠ ACВ < 90°.

4.Банк планирует вложить на один год 40% имеющихся y него средств клиентов в проект X , а остальные 60% — в проект Y . В зависимости от обстоятельств проект X может принести прибыль в размере от 19 до 24% годовых, а проект Y — от 29 до 34% годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке. Определите наименьший и наибольший возможный уровень процентной ставки по вкладам, при которых чистая прибыль банка составит не менее 10% и не более 15% годовых от суммарных вложений в проекты X и Y .

5.Функция f ( x ) определена на всей числовой прямой, является нечетной, периодической с периодом 4, и на промежутке 0 ≤ x ≤ 2 ее значения вычисляются по правилу f ( x ) = 1 − | x − 1|. Решите уравнение

2 f ( x ) f ( x − 8) + 5 f ( x + 12) + 2 = 0.

6.Найдите все значения параметра а , при которых периметр фигуры, заданной на координатной плоскости условием

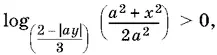
будет наименьшим.