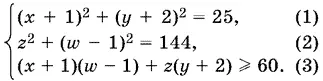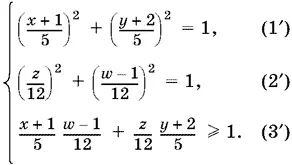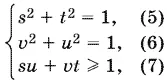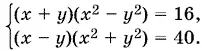Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Ответ.2 tg² α при 0 < α ≤ π/ 4, 2 ctg² α при π/ 4< α < π/ 2·

24.13.Введем обозначения: arcsin x = α, arccos x = β. Поскольку α + β = π/ 2, то

α³ + β³ = (α + β)³ − 3αβ(α + β) = π³/ 8− 3π/ 2αβ.

Наименьшее значение данной функции соответствует наибольшему значению произведения αβ. Так как β ≥ 0, то наибольшее значение αβ следует искать при α > 0. В этом случае (α > 0, β > 0) можно записать, что

αβ ≤ ( α + β/ 2)² = π²/ 16.

Наибольшее значение αβ достигается при α = β = π/ 4. Следовательно, наименьшее значение исходной функции достигается при x = 1/ √2и равно

π³/ 8 − 3π³/ 32= π³/ 32.

Наименьшее значение произведения αβ, где β ≥ 0, достигается при условии, что α < 0, причем желательно, чтобы абсолютные величины α и β были наибольшими. При x = −1 будет α = − π/ 2, β = π. Именно в этой точке произведение αβ достигает минимума, так как α принимает минимальное, а β — максимальное из возможных значений. Итак, при x = −1 исходная функция имеет наибольшее значение

π³/ 8 + 3π/ 2 π/ 2 π = 7π³/ 8.

Ответ. π³/ 32, 7π³/ 8.

24.14.Сделаем следующие преобразования:

y = 2 sin² x + 2 cos² x + 4(2 cos² x ) − 2 sin 2 x = 2 + 4(1 + cos 2 x ) − 3 sin 2 x = 6 + 4 cos 2 x − 3 sin 2 x = 6 + 5( 4/ 5cos 2 x − 3/ 5sin 2 x ) = (см. указание I) = 6 + 5(sin φ cos 2 x − cos φ sin 2 x ) = 6 + 5 sin(φ − 2 x ).

Поскольку min sin (φ − 2 x ) = −1, то min y = 6 − 5 = 1.

Ответ.1.

24.15.Преобразуем данную систему к виду

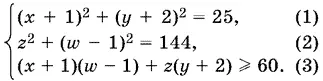
или

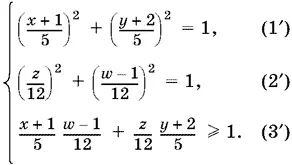
Введем новые переменные:

x + 1/ 5= s , y + 2/ 5= t , z / 12= v , w − 1/ 12= u . (4)

Тогда система примет вид

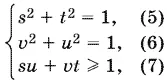
и для удовлетворяющих этой системе переменных нужно найти

min ( y + w ) = min (5 t + 12 u − 1). (8)

Обратим внимание на то обстоятельство, что (5) и (6) — уравнения окружностей радиуса 1. Поэтому можно положить:

s = sin α, t = cos α; v = sin β, u = cos β.

Тогда для левой части (7) получим

sin α cos β + sin β cos α = sin(α + β) ≤ 1. (9)

Учитывая соотношения (9) и (7) одновременно, получим

sin (α + β) = 1, т. е. α + β = π/ 2+ 2π k , (10)

или

sin α = cos β, cos α = sin β, (11)

s = u , t = v . (12)

Соотношение (7), которое преобразуется теперь в равенство, примет вид

u ² + t ² = 1. (13)

Нам нужно найти min (5 t + 12 u − 1). Воспользуемся соотношениями (11) и (12), в силу которых u = sin α, t = cos α. Тогда st − 12 u − 1 = 13( 5/ 13 − cos α − 12/ 13sin³ α) − 1 = 13 cos (α + φ) − 1, где cos φ = 5/ 13, sin φ = 12/ 13. Поэтому min (5 t − 12 u − 1) = −14.

Ответ.−14.

1.Сумма первых одиннадцати членов арифметической прогрессии 418. Найдите шестой член этой прогрессии.

2.Решите уравнение

cos 2 x = 2 − 2√3 cos x sin x .

3.Основанием наклонной треугольной призмы служит равносторонний треугольник. Сечение, проходящее через среднюю линию верхнего основания и одну из сторон нижнего основания, перпендикулярно основаниям призмы. Найдите объем призмы, если известно, что площадь сечения 30 м², а радиус окружности, описанной около основания, 10/ 3√3 м.

4.Решите систему уравнений

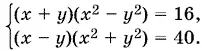
5.Решите неравенство

8(−2 x + 3 x )(−2 x − 1+ 3 x )(−2 x + 3 x + 1)(−2 x − 2+ 3 x ) + 81 x ≤ 0.

6.Сторона треугольника имеет длину 9 см, а радиус окружности, вписанной в этот треугольник, равен 3 см. Найдите наименьшее возможное значение, которое может достигать площадь данного треугольника.

1.Решите уравнение

|−sin x | = 2 cos x .

2.Решите неравенство

(9 x ² − 9 x + 2) log 23 x ≥ 0.

3.Разность цифр двузначного натурального числа A равна 4, а сумма квадратов цифр этого числа больше произведения его цифр на 37. Найдите число A .

4.Найдите сумму действительных корней уравнения

x ² + 2( с ² + 2 с ) x + 4 с ³ − 2 с ² + 40 = 0