Генри Дьюдени - Кентерберийские головоломки

Восемь первых полупутей – это от 1 до 6 (2 пути); от 1 до 8 (1 путь); от 1 до 10 (3 пути); от 1 до 12 (1 путь) и от 1 до 14 (1 путь). Восемь вторых полупутей: от 7 до 20 (1 путь); от 9 до 20 (1 путь); от 11 до 20 (3 пути); от 13 до 20 (1 путь) и от 15 до 20 (2 пути). Каждый новый способ, каким вы сумеете связать один полупуть с другим, даст новое решение задачи. Можно определить, что эти связи таковы: с 6 на 13 (2 случая); с 10 на 13 (3 случая); с 8 на 11 (3 случая); с 8 на 15 (2 случая); с 12 на 9 (1 случай) и с 14 на 7 (1 случай). Следовательно, существует 12 различных способов соединения и соответственно 12 различных решений нашей головоломки. Можно показать, что путь, приведенный на рисунке в условии задачи, состоит из одного из трех полупутей, идущих от 1 до 10, и полупути от 13 до 20. Стоит отметить, что 10 решений порождены пятью различными путями и их обращениями; другими словами, если вы отметите на рисунке эти 5 путей линиями, а затем перевернете рисунок вверх ногами, то получите 5 новых путей. Остальные два решения симметричны (в этих случаях 12 связано с 9, а 14 – с 7 ), и, следовательно, не порождают новых решений с помощью поворотов.

164. Изящное симметричное решение этой головоломки показано на рисунке. Каждый из четырех кенгуру совершает свою небольшую экскурсию и возвращается в свой угол, ни разу не прыгнув в клетку, посещавшуюся другим кенгуру, и не пересекая центральной прямой.

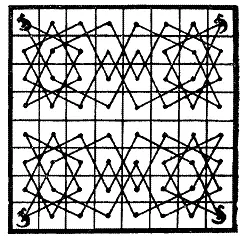
Читателю сразу же придет в голову возможность улучшить головоломку, разделив квадрат вертикальной прямой и потребовав, чтобы кенгуру не пересекали также и ее. Это означало бы, что каждый кенгуру ограничен квадратом 4×4, но это невозможно, как я покажу в решении следующих двух головоломок.

165. Пытаясь решить эту задачу, сначала необходимо взять два различных отсека соответственно из 20 и 12 клеток и проанализировать, где могут находиться здесь места входа и выхода. В случае большего отсека можно определить, что, желая совершить на нем полное турне, мы должны начать и закончить на двух внешних клетках длинных сторон. Но, хотя вы можете начинать на любой из этих 10 клеток, выбор конечной клетки ограничен, либо (что то же самое) вы можете заканчивать, где угодно, но тогда обязаны начинать путь на некоторых определенных клетках. В случае меньшего отсека вам придется начинать и заканчивать на одной из шести клеток, принадлежащих узким концам, а остальные ограничения такие же, как и в предыдущем случае. Небольшое размышление покажет, что в случае двух малых отсеков вы должны начинать и заканчивать в прилегающих друг к другу концах, а отсюда следует, что и в больших отсеках турне должно начинаться и заканчиваться на прилегающих сторонах.

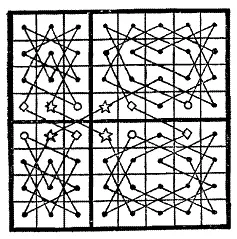
На рисунке, где показано одно из решений, можно заметить 8 мест, в которых мы можем начинать это конкретное турне; но в каждом случае существует лишь один путь, ибо мы должны закончить визиты в том отсеке, где находимся, прежде чем перейти в другой. Мы обнаружим, что в клетках, отмеченных звездочками, должны располагаться точки входа или выхода, но соображения, связанные с поворотами, наводят нас на мысль сделать другие соединения в местах, отмеченных либо ромбиками, либо кружочками. В решении, приведенном на рисунке, выбраны ромбики, но встречаются другие решения, где вместо них используются кружочки. Я думаю, что эти замечания поясняют все существенные моменты данной головоломки, которая весьма интересна и поучительна.

166.На рисунке показано, как шахматную доску можно разделить на 4 части одинаковых размеров и формы, чтобы на каждой из них можно было совершить турне конем.

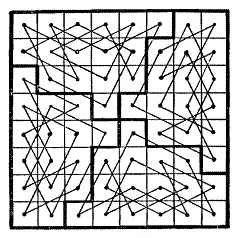
Для каждого коня существуют только один путь и его обращения.

167.Если бы читатель вырезал приведенную здесь диаграмму, сложил ее в форме куба и склеил с помощью полосок вдоль ребер, у него получилась бы довольно любопытная вещица.

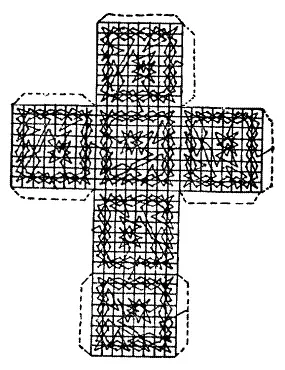
Ее можно выполнить в большем масштабе. Если мы представим себе, что на каждой грани куба расположена шахматная доска, то, как удается показать, мы можем начать в любой из 384 клеточек и совершить полное турне по кубу, вернувшись в конце в исходную точку. Метод перехода с одной грани на другую понять легко, но трудность, разумеется, состоит в том, чтобы определить нужные точки входа и выхода на каждой доске, порядок, в котором следует брать различные доски, и найти расположения, удовлетворяющие требуемым условиям.