Генри Дьюдени - Кентерберийские головоломки

Кстати сказать, расположения В можно добиться за 66 ходов, действуя следующим образом: 12, 11, 15, 12, 11, 8, 4, 3, 2, 6, 5, 1, 6, 5, 10, 15, 8, 4, 3, 2, 5, 10, 15, 8, 4, 3, 2, 5, 10, 15, 8, 4, 12, 11, 3, 2, 5, 10, 15, 6, 1, 8, 4, 9, 8, 1, 6, 4, 9, 12, 2, 5, 10, 15, 4, 9, 12, 2, 5, 3, 11, 14, 2, 5, 14, 11 = 66 ходов. Хотя это самое короткое решение, которое мне удалось найти, и я думаю, что более короткого не существует, я не могу это утверждать со всей определенностью. Наиболее привлекательным выглядит, конечно, расположение A, но вещи не таковы, какими кажутся, и достигнуть В оказывается легче всего.

Если бы можно было оставить свободной левую нижнюю камеру, то подошло бы следующее решение в 45 ходов, принадлежащее Р. Эрлику: 15, 11, 10, 9, 13, 14, 11, 10, 7, 8, 4, 3, 8, 6, 9, 7, 12, 4, 6, 9, 5, 13, 7, 5, 13. 1, 2, 13, 5, 7, 1, 2, 13, 8, 3, 6, 9, 12, 7, 11, 14, 1, 11, 14, 1. Но при этом передвигается каждый человек.

171. Сначала следует остановить свой выбор на наиболее обещающем пути коня, а затем попытаться достичь данного расположения за наименьшее число ходов. Я твердо держусь того мнения, что наилучшим будет расположение, представленное на рисунке, где, как можно заметить, каждое последующее число получается из предыдущего ходом коня, а пять собак (1, 5, 10, 15 и 20) никогда не покидают свои первоначальные конуры.

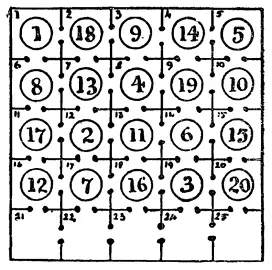
К этому расположению можно прийти за 46 ходов: 16–21, 16–22, 16–23, 17–16, 12–17, 12–22, 12–21, 7 – 12, 7 – 17, 7 – 22, 11–12, 11–17, 2–7, 2 – 12, 6 – 11, 8–7, 8–6, 13 – 8, 18–13, 11–18, 2 – 17, 18–12, 18 – 7, 18 – 2, 13 – 7, 3–8, 3 – 13, 4–3, 4–8, 9–4, 9–3, 14 – 9, 14 – 4, 19–14, 19 – 9, 3 – 14, 3 – 19, 6 – 12, 6 – 13, 6 – 14, 17–11, 12–16, 2 – 12, 7 – 17, 11–13, 16–18 = 46 ходов. Я, конечно, не могу категорически утверждать, что не существует решения с меньшим числом ходов, но думаю, что отыскать такое решение будет чрезвычайно трудно.

172.Назовем одну пешку А, а другую В. Далее, учитывая, что первый ход можно делать на одну или две клетки, мы получаем, что каждая пешка достигает восьмой клетки за 5 или 6 своих ходов. Следовательно, нужно рассмотреть четыре случая: (1) А и В делают по 6 ходов; (2) А делает 6, а В – 5 ходов; (3) А делает 5, а В – 6 ходов; (4) А и В делают по 5 ходов. В случае (1) делается 12 ходов, и мы можем отдать А любые 6 из них. Следовательно, 7×8×9×10×11×12, деленное на 1×2×3×4×5×6, [39]дает нам число комбинаций в этом случае, равное 924«Аналогично в случае (2) 6 ходов из 11 возможных дадут нам 462 варианта, в случае (3) 5 ходов из 11 возможных также дадут 462 варианта, а в случае (4) 5 ходов из 10 возможных дадут 252 комбинации. Складывая эти числа, мы получим 2100, что и является правильным ответом для данной головоломки.

173.Белые пешки можно расположить 40 320 способами, белые ладьи – 2 способами, белых коней – 2 способами и белых слонов – 2 способами. Перемножая эти числа, мы обнаружим, что белые фигуры можно расположить 322 560 различными способами. Черные фигуры можно, разумеется, расположить таким же числом способов. Следовательно, общее число различных расположений равно 322 560×322 560 = 104 044 953600. Но почти все просматривают то обстоятельство, что при каждом расположении саму доску можно поставить 2 способами. Следовательно, ответ нужно удвоить, что даст 208 089 907 200 различных способов.

174.Всего существует 1296 различных прямоугольников, из которых 204 являются квадратами, включая саму доску, а 1092 прямоугольника – не квадраты.

В общем случае доска п X п содержит (n 2+n) 2/4 прямоугольников, из которых (2n 3+ 3 п 2 + п )/6 квадратов и (3n 4+ 2n 3– 3 п 2– 2п)/ 12 прямоугольников, не являющихся квадратами. Стоит отметить тот любопытный факт, что общее число прямоугольников всегда равно квадрату треугольного числа со стороной п. [40]

175. Небольшая тонкость состоит в том, что в конечной позиции перенумерованные ладьи должны располагаться в правильном числовом порядке, но в направлении, противоположном тому, которое было на исходной диаграмме, иначе задача не разрешима. Ходите ладьями в следующем порядке их номеров. Поскольку всегда имеется лишь одна свободная клетка, на которую можно ходить (за исключением последнего хода), то наши обозначения не вызовут недоразумений: 5, 6, 7, 5, 6, 4, 3, 6, 4. 7, 5, 4, 7, 3, 6, 7, 3, 5, 4, 3, 1, 8, 3, 4, 5, 6, 7, 1, 8, 2, 1, ладья берет слона и делает мат. При этом делается наименьшее возможное число ходов, равное 32. Ходы короля черных вынуждены, и нет необходимости их здесь приводить.