Генри Дьюдени - Кентерберийские головоломки

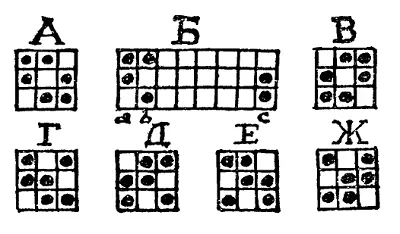
Я только упомяну, что А и Г – единственные два существенно различных расположения, поскольку если вы повернете А на четверть оборота, то получите В, а если вы станете поворачивать Г на четверть оборота по часовой стрелке, то получите последовательно Д, Е и Ж. Неважно, как вы располагаете свои пешки; если удовлетворяются условия головоломки, то вы обязательно получите одно из этих расположений. Разумеется, мы понимаем, что простое расширение не нарушает существенно характера этих расположений. Так, Б есть всего лишь расширенная форма А. Решение, следовательно, состоит в отыскании числа таких расширений. Предположим, что мы ограничились первыми тремя горизонталями, как в случае Б; тогда, поместив пары а и b на первых двух вертикалях, мы можем пару с расположить на любой из шести остальных вертикалей, что даст 6 решений. Теперь сдвинем пару b на третью вертикаль; тогда для пары с останется 5 возможных положений. Сдвинув b на четвертую вертикаль, мы оставим для с 4 возможности и так далее до тех пор (где а по-прежнему находится на первой вертикали), пока мы не сдвинем b на седьмую вертикаль, оставив для с единственное место на восьмой вертикали. Затем мы можем поместить а на второй, b на третьей, а с па четвертой вертикали и, сдвигая, как и прежде, с и b, находить серии новых решений.

Таким образом, мы получаем, что, пользуясь лишь схемой А и ограничивая себя только тремя верхними горизонталями, мы получаем столько ответов, сколько есть сочетании из 8 предметов по 3, то есть (8×7×6)/(1×2×3) = 56. Читатель сразу же догадается, что если можно 56 способами выбрать вертикали, то ровно столькими же способами в каждом из этих случаев можно выбрать горизонтали, ибо мы можем сдвигать пару сверху вниз точно так же, как и слева направо. Следовательно, общее число способов, подчиняющихся схеме А, равно 56×56 = 3136. Но, как мы уже видели ранее, существует 6 различных схем. Поэтому ответ равен 3136 X 6 = 18 816, как я и утверждал.

186.Ходите следующим образом: 3 – 11, 9 – 10, 1–2, 7 – 15, 8 – 16, 8–7, 5 – 13, 1–4, 8–5, 6 – 14, 3–8, 6–3, 6 – 12, 1–6, 1–9, и все шашки оказываются удаленными, за исключением /, что и требовалось в условиях задачи.

187.Ходите следующим образом: 7 – 15, 8 – 16, 8–7, 2 – 10, 1–9, 1–2, 5 – 13, 3–4, 6–3, 11 – 1, 14 – 8, 6 – 12, 5–6, 5 – 11, 31–23, 32–24, 32–31, 26–18, 25–17, 25–26, 22–32, 14–22, 29–21, 14–29, 27–28, 30–27, 25–14, 30–20, 25–30, 25 – 5. Две оставшиеся шашки – это 25 и 19; обе они принадлежат к одной группе, как и требовалось, причем 19 ни разу не сдвигается со своего исходного положения.

Я думаю, что невозможно придумать решение, где бы в конце игры на доске осталась только одна шашка.

188.

И получилась нужная позиция.

Порядок ходов не важен и может сильно меняться. Однако, несмотря на многочисленные попытки, число ходов уменьшить не удалось.

Гарднер М. Математические головоломки и развлечения. – М.: «Мир», 1971; Математические досуги. – М.: «Мир», 1972; Математические новеллы. – М.: «Мир», 1974.

Имеется в виду время, когда писалась книга, до метрической реформы в Англии, коснувшейся и денежных единиц. – Прим. перев.

Мадам, я Адам (англ.)

Ева (англ.).

Здесь и далее цитаты приводятся по книге: Джеффри Чосер, «Кентерберийские рассказы», перевод с англ. И, Кашкина и О. Румера, БВЛ, М.: «Художественная литература», 1973. Примечания переводчика, касающиеся реалий средневековой Англии, также основаны на примечаниях к данному изданию, сделанных И Кашкиным. – Прим. перев.

Йомен – лично свободный крестьянин, обязанный служить во время войны своему сюзерену. – Прим, перев.

Кентерберийские паломники ( англ.). – Прим. перев.

Франклин – зажиточный земельный собственник из старых деревенских англосаксонских родов. – Прим. перев.

Сквайром во времена Чосера называли оруженосца, который сопровождал рыцаря. – Прим. перев.