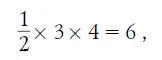Яков Перельман - Живая математика. Математические рассказы и головоломки

Итак, почему же передняя ось телеги стирается больше задней? Всем известно, что передние колеса меньше задних. На одном и том же расстоянии малый круг оборачивается большее число раз, чем круг покрупнее: у меньшего круга и окружность меньше - оттого она укладывается в данной длине большее число раз. Теперь понятно, что при всех поездках телеги передние ее колеса делают больше оборотов, нежели задние; а большее число оборотов, конечно, сильнее стирает ось.

65. Если вы полагаете, что в лупу угол наш окажется величиною в 1 1/ 4х 4 = 6°, то дали промах. Величина угла нисколько не увеличивается при рассматривании его в лупу.

Рис. 109. Передние колеса телеги меньше задних

Правда, дуга, измеряющая угол, несомненно, увеличивается, но во столько же раз увеличивается и радиус этой дуги, так что величина центрального угла остается без изменения. Рис. 109 поясняет сказанное. Невозможность увеличения углов лупой вытекает, между прочим, и прямо из того, что фигуры при рассматривании в лупу сохраняют геометрическое подобие самим себе. Если бы каждый угол многоугольника увеличивался в 4 раза, то мы видели бы в лупу квадраты с углами в 360° или треугольники, сумма углов которых равна 8 прямым!

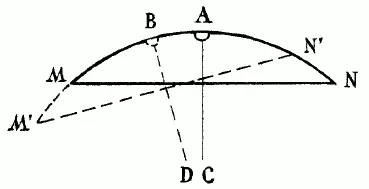
Рис. 110

66. Рассмотрите рис. 110, где MAN есть первоначальное положение дуги уровня, M’BN ’- новое ее положение, причем хорда JVPN' составляет с хордой MN угол в 1/ 2°. Пузырек, бывший раньше в точке А, теперь остался в той же точке, но середина дуги MN переместилась в В. Требуется вычислить длину дуги АВ, если радиус ее равен 1 м, а величина дуги в градусной мере 1/ 2° (это следует из равенства острых углов с перпендикулярными сторонами). Вычисление несложно. Длина полной окружности радиусом в 1 м (1000 мм) равна 2 х 3,14 х 1000 = 6280 мм. Так как в окружности 360°, или 720 полуградусов, то длина одного полуградуса определяется делением:

6280: 720 = 8,7 мм.

Пузырек отодвинется от метки (вернее, метка отодвинется от пузырька) примерно на 9 адм - почти на целый сантиметр. Легко видеть, что чем больше радиус кривизны трубки, тем уровень чувствительнее.

67. Задача вовсе не шуточная и вскрывает ошибочность обычного словоупотребления. У «шестигранного» карандаша не 6 граней, как, вероятно, полагает большинство. Всех граней у него, если он не очинен, 8: шесть боковых и еще две маленькие «торцовые» грани. Будь у него в действительности 6 граней, он имел бы совсем иную форму - бруска с четырех-угольным сечением. Привычка считать у призм только боковые грани, забывая об основаниях, очень распространена. Многие говорят: «трехгранная» призма, «четырехгранная» призма и т. д., между тем как призмы эти надо называть: треугольная, четырехугольная и т. д. - по форме основания. Трехгранной призмы, т. е. призмы о трех гранях, даже и не существует.

Поэтому карандаш, о котором говорится в задаче, правильно называть не шестигранным, а шестиугольным.

68. Сделать надо так, как показано на рис. 111.Получаются 6 частей, которые для наглядности перенумерованы.

69. Спички следует расположить, как показано слева на рис. 112;площадь этой фигуры равна учетверенной площади «спичечного» квадрата.

Как в этом удостовериться?

Дополним мысленно нашу фигуру до треугольника. Получится прямоугольный треугольник, основание которого равно 3, а высота 4 спичкам [25] Читатели, знакомые с так называемой «пифагоровой теоремой», поймут, почему мы с уверенностью можем утверждать, что получающийся здесь треугольник – прямоугольный: З 2 + 4 2 = 5 2 . . Площадь его равна половине произведения основания на высоту:

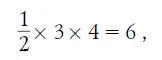
т. е. 6 квадратам со стороною в одну спичку. Но наша фигура имеет, очевидно, площадь, которая меньше площади треугольника на 2 «спичечных» квадрата и равна, следовательно, 4 таким квадратам.

Рис. 111

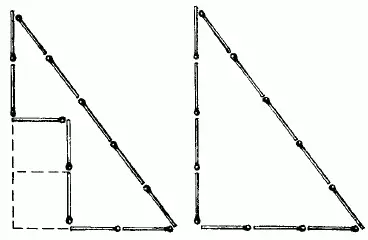
Рис. 112

Рис. 113