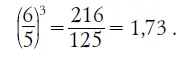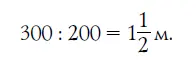Яков Перельман - Живая математика. Математические рассказы и головоломки

Почему же, однако, продавцы просят за такие арбузы обычно не вдвое, а только в полтора раза больше? Объясняется это просто тем, что продавцы в большинстве случаев не сильны в геометрии. Впрочем, не сильны в ней и покупатели, зачастую отказывающиеся из-за этого от выгодных покупок. Можно смело утверждать, что крупные арбузы выгоднее покупать, чем мелкие, потому что они расцениваются всегда ниже их истинной стоимости; но большинство покупателей этого не подозревают. По той же причине всегда выгоднее покупать крупные яйца, нежели мелкие, если только их не расценивают по весу.

82. Окружности относятся между собой как диаметры. Если окружность одной дыни 60 см, другой 50 см, то отношение их диаметров 60 х 50 = 6/ 5, а отношение их объемов

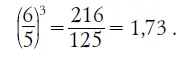
Большая дыня должна быть, если оценивать ее сообразно объему (или весу), в 1,73 раза дороже меньшей; другими словами, дороже на 73 %. Просят же за нее всего на 50 % больше. Ясно, что есть прямой расчет ее купить.

83. Из условия задачи следует, что диаметр вишни в 3 раза больше диаметра косточки. Значит, объем вишни больше объема косточки в 3 х 3 х 3, т. е. в 27 раз; на долю косточки приходится У часть объема вишни, а на долю сочной части - остальные 26/ 27- И, следовательно, сочная часть вишни больше косточки по объему в 26 раз.

84. Если модель легче натуры в 8 000 000 раз и обе сделаны из одного металла, то объем модели должен быть в 8 000 000 раз меньше объема натуры. Мы уже знаем, что объемы подобных тел относятся как кубы их высот. Следовательно, модель должна быть ниже натуры в 200 раз, потому что

200 х 200 х 200 = 8 000 000.

Высота подлинной башни 300 м. Отсюда высота модели должна быть равна

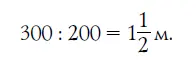
Модель будет почти в рост человека.

85. Обе кастрюли - тела геометрически подобные. Если большая кастрюля в 8 раз вместительнее, то все ее линейные размеры в два раза больше: она вдвое выше и вдвое шире по обоим направлениям.

Но раз она вдвое выше и шире, то поверхность ее больше в 2 х 2, т. е. в 4 раза, потому что поверхности подобных тел относятся как квадраты линейных размеров. При одинаковой толщине стенок вес кастрюли зависит от величины ее поверхности. Отсюда имеем ответ на вопрос задачи: большая кастрюля вчетверо тяжелее меньшей.

86. Эта задача, на первый взгляд вовсе не математическая, решается, в сущности, тем же геометрическим рассуждением, какое применено было в предыдущей задаче. Прежде чем приступить к ее решению, рассмотрим сходную с ней, но несколько более простую задачу.

I

Два котла (или два самовара), большой и малый, одинакового материала и формы, наполнены кипятком. Какой остынет скорее?

Вещи остывают главным образом с поверхности: следовательно, остынет скорее тот котел, в котором на каждую единицу объема приходится большая поверхность. Если один котел в п раз выше и шире другого, то поверхность его больше в п 1 раз, а объем - в п 3; на единицу поверхности в большем котле приходится в п раз больший объем. Следовательно, меньший котел должен остыть раньше. По той же причине и ребенок, стоящий на морозе, должен зябнуть больше, чем одинаково одетый взрослый: количество тепла, возникающего в каждом кубическом сантиметре тела, у обоих приблизительно одинаково, но остывающая поверхность тела, приходящаяся на каждый кубический сантиметр, у ребенка больше, чем у взрослого.

Также и пальцы рук или нос зябнут сильнее и отмораживаются чаще, чем другие части тела, поверхность которых не столь велика по сравнению с их объемом.

II

Сюда же, наконец, относится и следующая задача: почему лучина загорается скорее, чем толстое полено, от которого она отколота? Так как нагревание происходит с поверхности и распространяется на весь объем тела, то следует сравнить поверхность и объем лучины (например, квадратного сечения) с поверхностью и объемом полена той же длины и того же квадратного сечения, чтобы определить, какой величины поверхность приходится на 1 куб. см древесины в обоих случаях.

Если толщина полена в 10 раз больше толщины лучины, то боковая поверхность полена больше поверхности лучины тоже в 10 раз, объем же его больше объема лучины в 100 раз. Следовательно, на каждую единицу поверхности в лучине приходится вдесятеро меньший объем, чем в полене: одинаковое количество тепла нагревает в лучине вдесятеро меньше вещества, отсюда и более раннее воспламенение лучины, чем полена, от одного и того же источника тепла. (Ввиду дурной теплопроводности дерева, указанные соотношения следует рассматривать лишь как грубо приблизительные; они характеризуют лишь общий ход процесса, а не количественную сторону.)