Карлос Мадрид - Мир математики. т.32. Бабочка и ураган. Теория хаоса и глобальное потепление

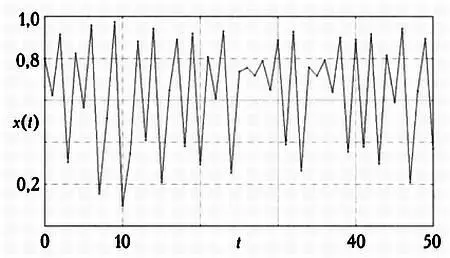
Орбита стала хаотической! В ней больше не наблюдается никаких закономерностей. Она даже не является квазипериодической, а «прыгает» с одного места на другое и кажется случайной. А что, если мы рассмотрим k= 4?

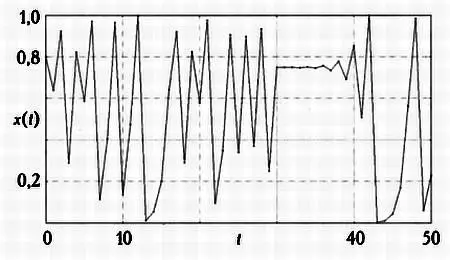
То же самое хаотическое поведение! Диаграмма-паутина будет хаотической, а представленные на ней значения будут беспорядочно колебаться между 0 и 1.

Однако орбита и диаграмма-паутина точки х 0= 0,8 — не исключение: все остальные возможные орбиты и диаграммы будут выглядеть точно так же. И вновь мы наблюдаем эффект карточной колоды.

На этом сюрпризы не заканчиваются: два различных начальных условия, близких друг к другу, определяют орбиты, которые по прошествии определенного времени будут выглядеть совершенно по-разному. Примем k = 4. Если мы хотим изучить орбиту точки а= 0,900 и по ошибке введем значение Ь= 0,901 (например, при измерении мы допустили ошибку, равную одной тысячной), то увидим, что орбиты а и b вскоре будут значительно отличаться, хотя изначально они были близки друг к другу. Орбита точки а будет образована значениями {0,900; 0,360; 0,9216; 0,2890; 0,8219; 0,5854; 0,9708…}, орбита точки b— значениями {0,901; 0,3568; 0,9180; 0,3012; 0,8419; 0,5324; 0,9958…}. Иными словами, исходная разница в одну тысячную через несколько итераций будет иметь порядок нескольких сотых. Всего за семь итераций разница увеличится в 20 раз! По прошествии определенного времени реальная и прогнозная траектории уже не будут иметь ничего общего.

И вновь мы наблюдаем эффект бабочки.

Подведем итог: изменяя значения параметра kв логистическом отображении от k = 2 до k= 4, мы показали, как система постепенно приближается к хаотическому состоянию. А где же операции растяжения и складывания, которые порождают хаос? Прямо у нас перед глазами. Логистическая функция f( х) = kx(1 — х) «растягивает» числовой интервал между 0 и 1 вследствие умножения хна k. Затем этот интервал «складывается пополам» в результате умножения kx на (1 — х) — число, меньшее единицы. Таким образом, числовой интервал растягивается и складывается, подобно подкове.

Хотя сегодня в математике не существует четкого определения детерминированного хаоса, он рассматривается как совокупность эффекта бабочки и эффекта карточной колоды, которые мы наблюдали и в сдвиге Бернулли, и в логистическом отображении Мэя.

От какого класса динамических систем стоит ожидать хаотического поведения?

Как вы уже знаете, хаос нужно искать среди нелинейных систем — только в них действие совокупности причин может не равняться совокупному действию этих причин по отдельности и приводить к совершенно неожиданным последствиям. Также (об этом мы не упоминали) нужно искать среди неинтегрируемых систем. Система называется интегрируемой, если ее траектории или решения можно явно выразить при помощи известных функций. Интегрируемые системы (линейные и нелинейные) предсказуемы, так как известна формула, позволяющая вычислить орбиту любой точки в любой момент времени. В неинтегрируемых системах, напротив, решение нельзя представить в виде формулы, поэтому для них нельзя составить прогноз на бесконечно большой период времени. Кроме того, если мы рассмотрим такие си¬стемы с точки зрения топологии, то увидим, что траектории будут тесно сплетаться между собой.

Если мы сведем две рассмотренные выше категории воедино, то увидим, что нелинейные и неинтегрируемые системы обладают беспорядочным, непредсказуемым поведением, указывающим на присутствие хаоса. Следует заметить: даже тогда, когда хаос требует нелинейности (чтобы небольшие изменения начальных условий могли вызывать значительные изменения) и неинтегрируемости (чтобы мы не могли делать прогнозы в долгосрочном периоде), нелинейная и неинтегрируемая динамика необязательно будет хаотической. Существуют нелинейные и неинтегрируемые системы, демонстрирующие равномерное и предсказуемое поведение. Математики говорят, что эти две характеристики — нелинейность и неинтегрируемость — являются необходимыми, но не достаточными.

С другой стороны, среди нелинейных и неинтегрируемых систем выделяют два подвида: гамильтоновы системы, сохраняющие энергию, и диссипативные, которые не сохраняют энергию. Этим двум видам систем соответствуют две разновидности детерминированного хаоса, известные сегодня.