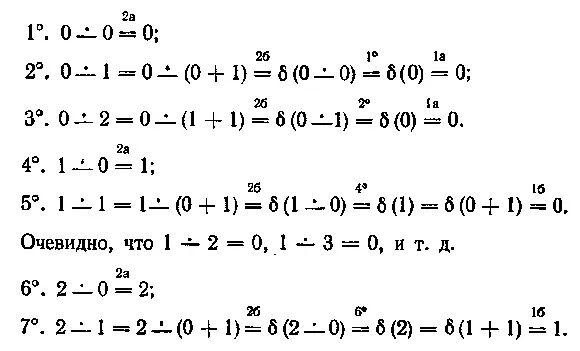Борис Бирюков - Жар холодных числ и пафос бесстрастной логики

1. Функция δ, определяемая условиями

а) δ(0)=0, б) δ(у+1)= y,

рекурсивна, как выраженная стандартной схемой рекурсии через исходные рекурсивные функции (здесь прибавление единицы к числу следует понимать как взятие следующего числа в натуральном ряду).

2. Функция х ∸ у, определяемая условиями

а) х ∸ О = х, б) х ∸ (у+1)=δ(х ∸ у),

рекурсивна, как выраженная стандартной схемой рекурсии через рекурсивную функцию δ. Как нетрудно убедиться, смысл функции х ∸ у (она называется усеченным вычитанием) таков: функция эта равна х — у, если х >= у и равна нулю, если х < у.

В самом деле, посмотрим, каково значение функции х ∸ у для х, у = 0, 1, 2, 3 (над знаками равенств помечаем какой пункт определений 1, 2 применяется или какое из ранее полученных значений функции х — у используется):

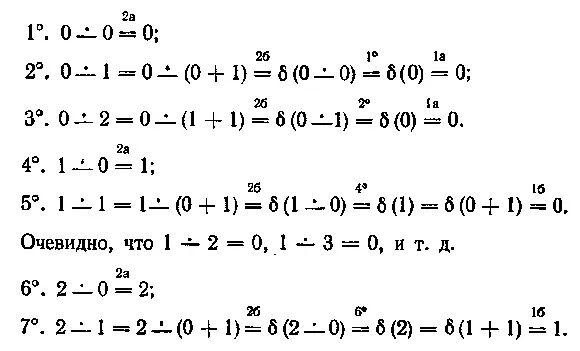
Подобным же образом вычисляется 0∸3=0,0∸4=0 (вообще, легко усматривается, что при дальнейшем возрастании значения у выражение 0 ∸ у будет оставаться равным нулю).

При дальнейшем возрастании значения y выражение 2 ∸ у становится равным нулю. Аналогично вычисляется, что 3 ∸ 0 = 3, 3 ∸ 1 = 2, 3 ∸ 2 = 1, но при y > 2 выражение 3 ∸ y равно нулю.

3. Предикат, опередляемый уравнением х ∸ у = 0, рекурсивен; это очевидно, поскольку функция х ∸ у, как мы показали, рекурсивна. Но смысл этого предиката выражается в обычном языке утверждением x <= у.

Далее, можно показать рекурсивность предиката строгого неравенства, так как для его выражения в формальной системе арифметики нужно использовать теперь только функцию взятия следующего числа («прибавление единицы»).

Несколько раньше введения рекурсивных функций Гёдель осуществляет важную процедуру, которая впоследствии была названа гёделевской нумерацией, или гёделизацией. Это — процедура нумерации всех символов, встречающихся в формальном арифметическом исчислении.

Сначала нумеруются знаки логических операций, вспомогательные символы и другие исходные знаки: символ 0 получает номер 1; символ f — номер 3; символ ~ — номер 5; символ V — номер 7; символ Ɐ — номер 9; символ ), то есть левая скобка, — номер 11; символ ), то есть правая скобка, — номер 13. Таким образом, для нумерации исходных знаков используются нечетные числа от 1 до 13. Символы импликации, конъюнкции и эквиваленции и квантор существования в исчислении Гёделя не фигурируют; эти логические операции могут быть выражены через отрицание, дизъюнкцию и квантор общности.

Далее нумеруются переменные x1, у1, z1,..., вместо которых в арифметические формулы подставляются числа. Для этого используются простые числа, начиная с 17. Аналогичным способом нумеруются предикатные переменные x2, y2, z2,... (переменные, на места которых в формулах подставляются знаки свойств и отношений), только для нумерации используются квадраты простых чисел, начиная с 17 (символ х2 получает номер 17 2, символа y2— номер 19 2и т. д.).

Затем следует нумерация последовательностей символов (частным случаем которых являются формулы). Здесь правило присвоения номеров таково: если имеется последовательность из k символов, имеющих номера соответственно n1, n2, ... nk, то номер этой последовательности имеет вид: 2 n1* З n2* 5 n3- ... pk nk, где pk — k-тое простое число, начиная с двух. Покажем наглядно, как «работает» в этом случае гёделизация. Пусть дана формула Vх1(х2(х1)) (она читается: «Для всякого натурального числа x1 выполняется свойство х2). Найдем ее гёделев номер. Выпишем по порядку гёделевы номера входящих в формулу символов: 9, 17,11,289,11,17,13,13. Номер N рассматриваемой формулы таков:

N=2 9• З 17• 5 11• 7 289• 11 11• 13 17• 17 18• 19 13.

Наконец, нумеруются последовательности формул. Если дана последовательность из 5 формул с номерами m1, m2, m3..., m s, то номер последовательности определяется как 2 m1• 3 m2• 5 m3• ... • p s ms, где p s— 5-тое простое число.

Используя рекурсивные функции, Гёдель показывает, что с помощью проведенной нумерации все «метаарифметические» высказывания, то есть высказывания об арифметических объектах, можно представить как соотношения между числами (гёделевыми номерами). Скажем, утверждение «Данная комбинация символов есть формула» выражается некоторым арифметическим предикатом от гёделева номера этой комбинации n, то есть записывается в виде некоторой арифметической формулы q2n.

Аналогично, утверждение «Данная последовательность формул является доказательством» предстает в виде арифметического предиката от номера этой последовательности. Показывается, что арифметизируются и высказывания вида: «Данная формула есть результат подстановки в такую-то формулу вместо такой-то переменной такой-то формулы», «Данная формула доказуема» (то есть существует последовательность формул, являющаяся доказательством, которая кончается на данной формуле) и т. д. Проведя такую работу, Гёдель показал фактически, что исчисление можно значительно «ужать», эаменив символы, формулы и доказательства некими представляющими их числами, а утверждения о формулах можно превратить в арифметические формулы.