Рауль Ибаньес - Мир математики - т.6 Четвертое измерение. Является ли наш мир тенью другой Вселенной?

Трехмерные сечения гиперсферы (рисунок Хосу Арройо).

Если рассекать куб вдоль одной из его граней, другими словами, делать параллельные срезы, то полученные сечения будут квадратами, как видно на рисунке на следующей странице. Если сделать срез, проходящий через одно из ребер по диагонали куба, и другие сечения, параллельные этому срезу, то получаются прямоугольники, квадраты и отрезки. Самые интересные сечения, которые труднее всего представить, получаются, когда делаются срезы, начиная с одной из вершин и перпендикулярно к диагонали куба, соединяющей эту вершину с противоположной.

Сначала получается треугольник, который увеличивается в размерах, затем уменьшается, пока не исчезнет на противоположной вершине. Но какую фигуру мы увидим в середине этого процесса? Как ни странно, это правильный шестиугольник, то есть шестиугольник с равными сторонами и углами.

Это происходит потому, что треугольные сечения изменяются при прохождении через другие три вершины куба, образуя шестиугольник со сторонами разной длины, который потом снова становится треугольником, уменьшающимся в размере.

Но вершины этого треугольника теперь ориентированы в направлении, противоположном направлению изначального треугольника, поэтому в силу симметрии в средней точке мы получаем правильный шестиугольник.

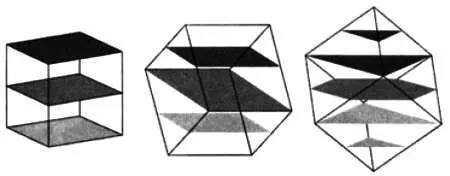
Плоские сечения куба в зависимости от направления среза.

* * *

ГОРИЗОНТАЛИ

Плоские сечения трехмерных объектов с целью получения информации об их геометрии и форме используются, например, в топографии. На топографических картах можно видеть различные контуры, которые представляют собой точки, находящиеся на одной высоте над уровнем моря. Они показывают горизонтальные сечения поверхности местности на различной высоте. При пересечении поверхности горизонтальными плоскостями как раз и получаются такие кривые линии. Если они расположены очень близко друг к другу, то на местности это означает наличие крутого склона, а если они находятся далеко друг от друга, то поверхность более пологая. Горизонтали наряду с использованием цвета на топографических картах дают дополнительную информацию о рельефе.

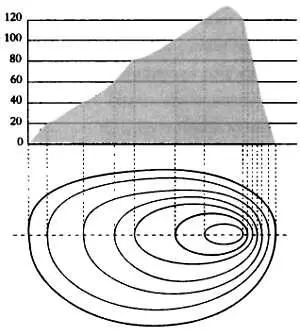
Горизонтали служат для изображения рельефа местности.

* * *

Чтобы получить трехмерные сечения гиперкуба, мы, как и в случае с кубом, будем делать срезы вдоль кубической грани, затем параллельно квадратной грани, затем параллельно ребру и, наконец, начиная с вершины. Можно представить, будто гиперкуб падает сквозь наше трехмерное пространство. Мы будем изучать те части гиперкуба, которые мы видим во время его движения.

Если принять во внимание, что гиперкуб, или тессеракт, представляет собой куб, движущийся в дополнительном перпендикулярном направлении, то очевидно, что его трехмерные сечения вдоль кубической грани всегда являются кубами. И действительно, эти сечения — различные положения трехмерного куба при его движении в четвертом измерении.

Чтобы понять, как выглядят сечения гиперкуба при срезах параллельно квадратной грани, надо представить сечения куба вдоль его граней или ребер. Как видно на рисунке ниже, квадратная грань образует квадратные сечения при движении, в то время как кусочки рассекаемой квадратной грани образуют прямоугольники, поэтому сечения гиперкуба будут представлять собой прямоугольные призмы с квадратными основаниями.

Сечения куба со стороны ребра и вершины помогают понять форму трехмерного сечения гиперкуба при срезах параллельно ребру. Последовательность трехмерных срезов будет линией, треугольной призмой, затем шестиугольной призмой и правильной шестиугольной призмой. Затем эти фигуры будут повторяться в обратном порядке.

Наиболее интересный случай, как и в примере с кубом, — это сечения гиперкуба, начиная с его вершины. Последовательность сечений представляет собой точку, тетраэдр, усеченный тетраэдр, икосаэдр, снова усеченный тетраэдр, тетраэдр и опять точку.