Рауль Ибаньес - Мир математики - т.6 Четвертое измерение. Является ли наш мир тенью другой Вселенной?

Существует два типа проекций — геометрические и алгоритмические. Первый является более естественным, его можно интерпретировать как лучи света, дающие изображения и тени. Алгоритмические проекции выражаются с помощью математических формул. Это означает, что геометрическая интерпретация теряется, зато можно использовать мощные математические средства.

В этой главе мы рассмотрим два типа естественных геометрических проекций, используемых в повседневной жизни. Это ортогональные проекции, соответствующие освещению солнечным светом, и центральные проекции, связанные с близко расположенным источником света, например лампой или фонарем. Именно так работает наше зрение, и именно их имитирует перспектива в живописи.

* * *

АЛГОРИТМЫ И АЛГОРИФМЫ

Алгоритм — это упорядоченный и конечный набор действий для решения задачи, будь то в области математики или других наук. Метод вычислений также называется алгоритмом. Раньше в качестве синонима слова «алгоритм» использовали слово «алгорифм», однако в наши дни такое написание практически не употребляется, за исключением устойчивых выражений, как, например, «Нормальный алгорифм Макарова». Математик А.А. Макаров (младший) (1903–1979) был основоположником советской школы конструктивной математики и ввел понятие нормального алгоритма.

* * *

Для начала вспомним, как мы в детстве рисовали куб. Наверняка наши изображения были похожи на рисунок слева. Но мы тогда и не подозревали, что рисуем ортогональную проекцию куба.

Ортогональная проекция — это отображение, а именно проецирование в определенном направлении n-мерного координатного пространства любой размерности nна одно из его подпространств ( n— 1) размерности. Иными словами, все точки, которые находятся на одной прямой линии, расположенной в заданном направлении, проецируются в одну точку (n — 1) — мерного подпространства, в которой эта прямая линия пересекает подпространство. В трехмерном пространстве подпространство, на которое мы проецируем, является плоскостью. Образ объекта, полученный в результате ортогонального проецирования, представляет собой своего рода тень объекта, полученную при освещении его параллельными лучами света, падающими на плоскость проекции в заданном направлении (см. рисунок ниже). Например, так как Солнце находится очень далеко от Земли, солнечные лучи можно считать параллельными, и они падают на Землю в определенном направлении. Таким образом, тени предметов являются ортогональными проекциями. Конечно, если изменить направление проецирования, то получаются различные плоские проекции одного и того же объекта.

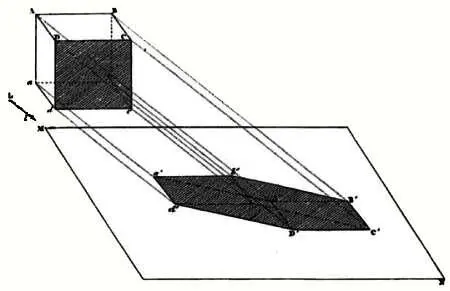
Ортогональная проекция куба из «Начертательной геометрии» французского математика Гаспара Монжа.

Рассмотрим теперь трехмерный куб и спроецируем его на плоскость. Чтобы лучше представить проекцию, возьмем кубическую рамку — стержни, показывающие структуру куба и представляющие линии, из которых состоит куб. Проецируя в разных направлениях, мы получим следующие изображения. Как видим, они очень хорошо отражают интуитивный подход, который мы использовали на протяжении всей книги: куб — это результат перемещения квадрата в перпендикулярном направлении.

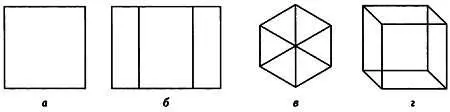
Ортогональные проекции куба в следующих направлениях: а — перпендикулярном к двум граням куба и параллельном четырем другим; б— параллельном только верхней и нижней граням куба; в— параллельном диагонали; г— не параллельном ни граням, ни диагонали.

В этом случае хорошо видно свойства ортогональных проекций: они переводят отрезки прямых в отрезки или точки и сохраняют параллельность. Кроме того, параллельные отрезки равной длины проецируются в параллельные отрезки также равной длины.

Если мы теперь ортогонально спроецируем четырехмерный гиперкуб (точнее, его каркас) на трехмерное пространство, мы получим трехмерную фигуру, изображенную на рисунке ниже.

Ортогональная проекция каркаса гиперкуба на трехмерное пространство, сделанная с помощью конструктора Zometool.