Рауль Ибаньес - Мир математики - т.6 Четвертое измерение. Является ли наш мир тенью другой Вселенной?

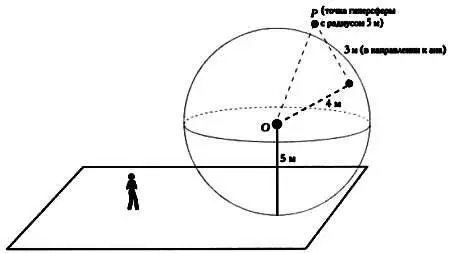
Сфера с центром Ои радиусом 5 м является частью гиперсферы, той частью, которая находится в нашей трехмерной вселенной. Если мы отойдем от центра сферы на 4 м, а затем на 3 м в направлении к ана, то окажемся в точке Р, которая будет точкой гиперсферы с радиусом 5.

Так можно получить все точки гиперсферы. Чтобы лучше понять эту идею, мы повторим этот процесс на поверхности Флатландии. Предположим, что Квадрат, главный герой книги Эбботта, захотел изобразить на плоскости сферу с центром в точке Ои радиусом 5. Сначала он нарисовал в своей плоской вселенной окружность радиуса 5, которая, как он знает, является частью трехмерной сферы, то есть той частью, которая находится во Флатландии. Затем он действует так же, как и мы: он перемещается в любом направлении от центра на расстоянии 4 м, а затем представляет движение на 3 м вверх. По теореме Пифагора (которую он, к счастью, знает) полученная точка также будет точкой сферы (см. рисунок ниже). Кроме того, из точек окружности меньшего радиуса, например 4 м, Квадрат может представить другую окружность в верхней части сферы (то есть плоское сечение сферы), расположенную в 3 м над Флатландией. Другая меньшая окружность может быть получена при движении вниз.

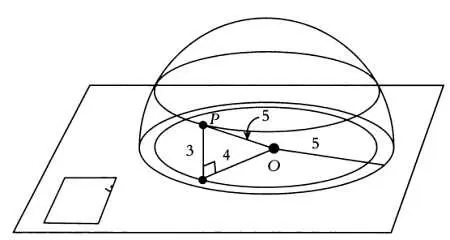
Окружность с центром Ои радиусом 5 м, нарисованная Квадратом, является той частью сферы, которая находится во Флатландии. Если мы переместимся от центра круга на расстояние 4 м, а затем на 3 м вверх, то мы окажемся в точке Р, которая также будет точкой сферы радиуса 5 м.

Квадрату удалось понять, что такое сфера, но теперь он должен попытаться представить ее. Учитывая, что каждая окружность с центром Ои радиусом меньше 5 м соответствует окружности сферы (на самом деле двум окружностям), квадрат-математик представляет себе половину сферы как группу всех окружностей с центром О и радиусом меньше 5 м, как показано на рисунке.

Полусфера, изображенная на плоскости в виде плоских окружностей с радиусами меньшими, чем радиус сферы (рисунок Хосу Арройо).

Квадрат может мысленно представить себе это изображение, но все еще с большим трудом, поэтому он идет дальше и разделяет все круги по длине отрезка (отрезка прямой линии с концами —5 и 5) так, что каждая точка отрезка обозначает высоту hот плоскости: положительная — вверх, отрицательная — вниз. Круг, соответствующий этой точке, будет кругом сечения сферы на высоте h(радиус которого равен положительному числу с, вычисляемому по теореме Пифагора: h 2+ с 2= 5 2). Следующий рисунок получен именно так.

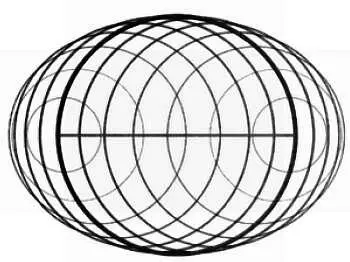
Точки, находящиеся на отрезке, указывают высоту, на которой расположена каждая из окружностей. Этот рисунок является визуализацией сферы на плоскости (рисунок Хосу Арройо).

Возвращаясь к случаю гиперсферы радиуса 5 м в четвертом измерении, мы можем применить аналогичный метод и представить полугиперсферу как семейство всех сфер с центрами на вершине мачты и с радиусами, меньшими 5 м или равными 5 м. Мы можем представить гиперсферу как все сферы, расположенные на различных высотах hв направлении ана или ката.

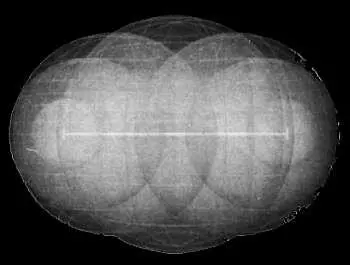
Все сферы в направлении, перпендикулярном к трехмерному пространству (в направлении ана или ката), являющиеся частями гиперсферы, изображены на отрезке, точки которого указывают высоту каждой сферы. Этот рисунок является визуализацией гиперсферы в нашем трехмерном пространстве (рисунок Хосу Арройо).

Одним из методов, используемых для визуализации четырехмерного объекта, в данном случае гиперкуба, в трехмерном или даже в двумерном пространстве, являются математические проекции, которые преобразуют четырехмерное пространство в трехмерное. Как правило, мы можем использовать математические проекции для преобразования любого n-мерного пространства в пространства меньших размерностей.