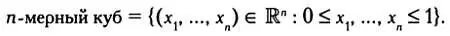Рауль Ибаньес - Мир математики - т.6 Четвертое измерение. Является ли наш мир тенью другой Вселенной?

Эти методы уже были известны и широко использовались в начале XX в. Описывая различные методы визуализации, мы будем опираться на интуицию и, как и в других главах книги, использовать многомерные аналогии.

Гиперкуб, также известный как тессеракт (термин, введенный Чарльзом Хинтоном в книге «Новая эра мысли»), является обобщением куба в четвертом измерении.

Как и в первой главе, предположим, что точка, имеющая нулевую размерность, будет также 0-мерным кубом, то есть кубом в нулевом измерении. Если точка находится на прямой линии (в одномерном пространстве) и перемещается на определенное расстояние по этой прямой, то мы получим отрезок (который будет одномерным кубом). Если точка находилась в начале оси координат и переместилась на единицу вправо, то полученный отрезок будет отрезком [0, 1], другими словами, он состоит из всех точек между 0 и 1 (см. рисунок на странице 106). Если этот отрезок находится на оси X координатной плоскости, то, перемещая его на одну единицу по оси Y, перпендикулярной оси X, мы получим квадрат (двумерный куб) со сторонами 1.

Если мы переместим единичный квадрат на одну единицу в перпендикулярном направлении к плоскости ХУ по оси Z, то мы получим трехмерный куб. Перемещая трехмерный куб в направлении, перпендикулярном к трем остальным, по новой оси, которую мы будем называть W, мы, наконец, получим гиперкуб, или четырехмерный куб.

В нашем пространстве мы не можем визуализировать гиперкуб, поэтому мы будем представлять куб, перемещающийся в перпендикулярном направлении к трехмерному пространству, как показано на с. 106.

* * *

ПОМОГАЮТ ЛИ ТРЕХМЕРНЫЕ ПРОЕКЦИИ ВИЗУАЛИЗИРОВАТЬ ЧЕТВЕРТОЕ ИЗМЕРЕНИЕ?

Многие считают, что невозможно полностью представить четырехмерный объект в трех измерениях, а тем более в двух. Это в некоторой степени правда, хотя, с другой стороны, люди привыкли представлять окружающий мир в двух измерениях с помощью картин, фотографий и кино. Другими словами, мы не подвергаем сомнению достоверность плоских изображений реальности. Более того, для получения информации о реальности эти двумерные изображения иногда просто необходимы, если учитывать изменение ракурсов и моментов времени. Приведем пару несложных примеров. Театр теней, например, несмотря на простоту плоских черных силуэтов, не мешает нам узнавать форму предметов и следить за сюжетом пьесы.

Вторым известным примером является бег лошади. Вплоть до 1870 г. завсегдатаи калифорнийских скачек вели дебаты о том, существует ли такой момент, когда ни одно из копыт лошади не касается земли. Спор был решен после того, как британский фотограф Эдвард Мейбридж(1830–1904) сделал ряд снимков, на которых было видно, что такой момент действительно существует.

Серия фотоснимков Мейбриджа, показывающих движение лошади. В один из моментов копыта лошади не касаются земли.

* * *

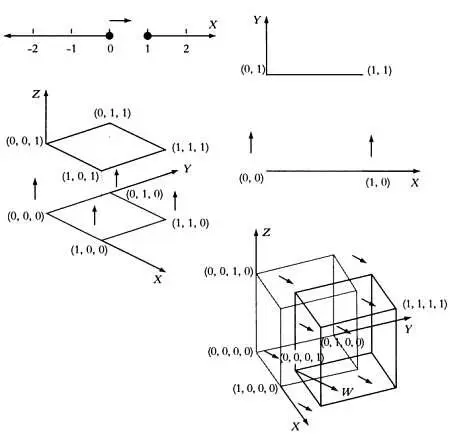
Отрезок прямой, квадрат, куб и гиперкуб со стороной 1 в соответствующих пространствах.

Интуитивно понятно, что каждый n-мерный куб, то есть куб в n-м измерении, получается путем перемещения (n — 1) — мерного куба из измерения на единицу меньше в направлении, перпендикулярном к предыдущим. Однако в математических терминах n-мерный куб может быть задан всеми точками в n-мерном пространстве, координаты которых больше 0 и меньше 1, то есть:

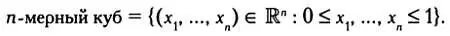
Каждый n-мерный куб состоит из элементов меньших размерностей — k-мерных кубов, где 0 <= k <= n. Например, гиперкуб состоит из следующих элементов: точек (вершин или углов), отрезков (ребер), граней (квадратных поверхностей), кубов (кубических граней) и самого гиперкуба. Для того чтобы попытаться понять, что такое гиперкуб, мы начнем с анализа элементов, из которых он состоит, используя следующие рассуждения и аналогии (с помощью рисунка).

Рассмотрим сначала элементы одномерного куба, то есть отрезка прямой линии.

Отрезок состоит из двух вершин и, конечно, самого себя. Теперь, переместив отрезок в перпендикулярном направлении и получив квадрат, мы имеем две начальные вершины и две конечные, следовательно, число вершин при перемещении удвоилось. Таким образом, квадрат имеет 4 вершины, куб — 8, а гиперкуб — 16. Теперь посчитаем ребра квадрата. У нас был начальный отрезок, затем конечный плюс два отрезка, образованные при перемещении каждой вершины, поэтому квадрат имеет 1 + 1 + 2 = 4 ребра. Аналогично куб будет иметь 4 + 4 + 4 = 12 ребер, а гиперкуб — 12 + 12 + 8 = 32 ребра.