Рауль Ибаньес - Мир математики - т.6 Четвертое измерение. Является ли наш мир тенью другой Вселенной?

Ключевым моментом в решении этого вопроса стала работа итальянского математика Джироламо Саккери (1667–1733). Вместо того чтобы вывести пятый постулат из предыдущих, он использовал метод от противного. Доказательство основывалось на четырехугольнике с двумя прямыми углами А и D и равными сторонами АВ и CD. Для других равных углов В и С существует три возможности:

1) В = С = 90° (гипотеза прямых углов, или евклидова гипотеза);

2) В = С > 90° (гипотеза тупых углов);

3) В = С < 90° (гипотеза острых углов).

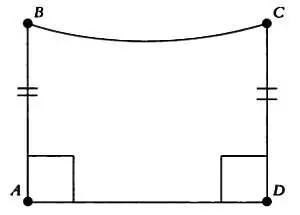
Четырехугольник Саккерис двумя прямыми углами.

Гипотеза тупых углов быстро отбрасывается, о гипотезе острых углов Саккери сказал следующее: «Гипотеза острых углов абсолютно ложна, потому что противна самой природе прямой линии». И Саккери, и немецкий математик Иоганн Генрих Ламберт (1728–1777) получили интересные геометрические результаты, вытекающие именно из гипотезы острых углов.

Лишь в XIX в. Гаусс, Лобачевский и Бойяи окончательно решили эту проблему, хотя немецкий математик Иоганн Карл Фридрих Гаусс не публиковал свои открытия, поскольку они противоречили философским доктринам той эпохи о природе пространства.

Русский математик Николай Иванович Лобачевский был первым, кто обнародовал новую геометрию, отличавшуюся от геометрии Евклида. Лобачевский назвал ее «воображаемой геометрией», и теперь она известна как гиперболическая геометрия. Она соответствует гипотезе острых углов Саккери, по которой через точку вне данной прямой проходит бесконечное количество прямых, параллельных данной.

Лобачевский представил свою работу в 1826 г. на конференции в Казанском университете, где он работал, а затем опубликовал ее в журнале «Казанский вестник» в серии статей под названием «О началах геометрии». Три важнейшие его работы содержат описание новой геометрии: «О началах геометрии» (на русском языке), «Геометрические исследования по теории параллельных линий» (на немецком языке) и его последняя книга «Пангеометрия» (на русском и французском языках).

Математик-любитель и офицер австро-венгерской армии Янош Бойяи (1802–1860) подошел к задаче с несколько иной точки зрения. Он разработал абсолютную геометрическую теорию, используя только первые четыре постулата, и исследовал, зависят ли полученные геометрические результаты от пятого постулата. Его статья была опубликована в 1832 г. в виде приложения к работе его отца, близкого друга Гаусса, математика Фаркаша Бойяи (1775–1856), который также работал над проблемой о параллелях. Он так написал об этом своему сыну: «Ради бога, молю тебя, оставь эту материю. Страшись ее не меньше, нежели чувственных увлечений, потому что и она может лишить тебя всего твоего времени, здоровья, покоя, всего счастья твоей жизни…»

* * *

ИММАНУИЛ КАНТ И ЕВКЛИДОВА ГЕОМЕТРИЯ

После эпохи Возрождения образ Бога начал терять свое значение в области математики и науки в целом. Позже, в XVIII в., роль Бога как архитектора мира еще более поблекла. Говорят, что Наполеон упрекал французского математика Пьера Лапласа (1749–1827) в том, что в его главной работе «Небесная механика» тот не упоминал Творца, на что Лаплас ответил: «Сир, я не нуждался в этой гипотезе».

Но тогда философы задались вопросом, а верны ли сами математические законы природы?

Шотландский философ Дэвид Юм(1711–1776) считал, что наше знание о мире является субъективным, поскольку оно получено через наши органы чувств. Другими словами, никто не может гарантировать существование объективного физического мира, и, следовательно, не имеет смысла говорить о его научных законах.

Со своей стороны, Кант в работе «Критика чистого разума» (1781) утверждал, что пространство и время являются формами восприятия и интуиции, на основании которых ум рассматривает реальность. Так как понятие пространства находится в нашем сознании, оно принимает форму определенных истин, которые Кант называл «априорными синтетическими суждениями», являющимися частью наших врожденных умственных способностей. Геометрия просто следует из них. Евклидова геометрия и трехмерное пространство являются частью этих истин априори.

* * *

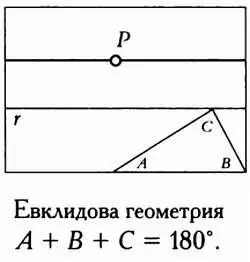
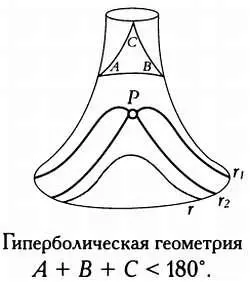
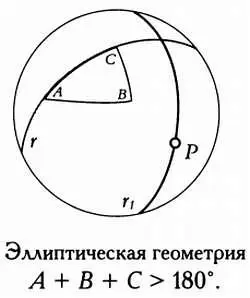
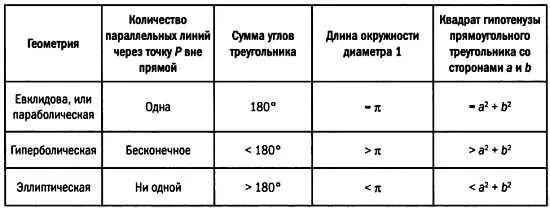
И сумма углов треугольника, и количество прямых, параллельных данной прямой линии и проходящих через точку вне ее, зависит от типа геометрии: евклидовой, гиперболическойили эллиптической.