Рауль Ибаньес - Мир математики - т.6 Четвертое измерение. Является ли наш мир тенью другой Вселенной?

Теория струн до сих пор не доказана экспериментально, хотя уже произвела глубокую научную и философскую революцию. Ее противники утверждают, что ее невозможно полностью проверить и, следовательно, в действительности она вообще не является научной теорией. Это один из вопросов, на который может пролить свет Большой адронный коллайдер, построенный в ЦЕРНе.

В области математической физики важность работы с многомерными пространствами уже давно стала очевидной. Французский математик Жозеф Луи Лагранж (1736–1813) в своей книге «Аналитическая механика» рассматривал механику в терминах многих координат (степеней свободы), включая время как отдельную координату. Впоследствии ирландский математик и астроном Уильям Роуэн Гамильтон (1805–1865) переписал уравнения механики для многомерных пространств.

Давайте рассмотрим следующий пример. Нам нужны четыре координаты для описания положения колеса, которое без скольжения движется вперед по поверхности: две координаты для описания точки касания колеса с поверхностью, одна — для угла поворота, и еще одна — для угла вращения вокруг продольной оси. Это делает пространство положений колеса четырехмерным. Если мы добавим движение, нам придется ввести еще четыре координаты для скорости. Таким образом, пространство положений колеса, движущегося по поверхности, имеет восемь измерений.

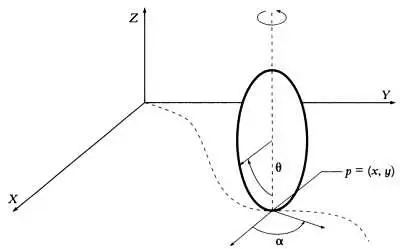
Эта диаграмма показывает, что пространство положений колеса, которое катится без скольжения по плоской поверхности, имеет четыре измерения. Координаты точек — х, у, α, Θ. Первые две, хи у, описывают точку касания колеса с плоскостью. Угол αявляется углом вращения вокруг продольной оси, а Θ— углом поворота.

Большинство областей науки (физика, астрономия, экономика, биология, медицина, машиностроение и многие другие) используют многомерные пространства.

Значение такого подхода заключается в том, что он позволяет нам оперировать геометрическими и математическими инструментами для получения полезной информации по изучаемому объекту или для выявления его интересных применений. Рассмотрим два ярких примера, которые показывают полезность этих методов в нашей повседневной жизни.

Шифрование сообщений

Мобильные телефоны, интернет, цифровые телевизоры, музыкальные компакт-диски, фильмы на DVD, цифровая идентификация — все это зависит от шифрования данных и их последующей расшифровки. В этом процессе обнаружение и исправление ошибок является важным элементом.

В наш цифровой век шифрование сообщений, будь то изображение, музыка или текст, требует перевода информации в последовательности нулей и единиц. Это называется двоичным шифрованием (каждый 0 или 1 называется бит — сокращение от английского выражения «двоичная цифра»). Такие последовательности делятся на «слова» фиксированной длины, которую мы обозначим k. Строки из 4 бит (содержащие 4 цифры) называют шестнадцатеричными цифрами. Всего существует 24 = 16 таких цифр, а строки из 8 бит называются байтами (их 28 = 256 штук).

Кодировка ASCII содержит 256 возможных кодов для выражения различных символов, другими словами, с помощью этих кодов можно закодировать 256 печатных символов. Бит каждого «слова» можно рассматривать как координату, хотя она принимает только значения 0 и 1. Каждое «слово» из kбит представляет собой точку в координатном пространстве размерности k, другими словами, количество размерностей равно длине слов. Например, шестнадцатеричное слово ООН отождествляется с точкой (0, 0, 1, 1) четырехмерного координатного пространства. В этом пространстве можно задать расстояние — способ измерения, насколько далеко друг от друга находятся точки (двоичные «слова») этого геометрического пространства.

Например, так называемое расстояние Хэмминга между двумя словами определяется количеством цифр, которыми эти слова различаются (так, слова ООН и 1011 находятся на расстоянии 1). В этом координатном пространстве мы можем использовать все математические инструменты арифметики, алгебры, анализа и геометрии.

Однако все не так просто, учитывая, что при передаче данных — со спутника или по электронной почте — или при чтении зашифрованных данных (например, на музыкальных компакт-дисках) могут возникнуть ошибки. В этой ситуации у нас имеется две проблемы: возможно, мы не знаем, что полученная информация является ошибочной, а также мы не знаем, какие биты неправильны. Поэтому приходится использовать дополнительные контрольные коды, увеличивая длину слов и, следовательно, размерность координатного пространства.