Хавьер Фресан - Мир математики - m. 35 Пока алгебра не разлучит нас. Теория групп и ее применение.

ЛЕВИ-СТРОСС: Рассмотрим оставшийся случай, когда дочери придерживаются той же формулы заключения брака, что и родители, сыновья — обратной, следовательно, р = 1, q = 0. Таким образом, функции f и g будут равны:

f(а, b, с, d) = (а+1, b+1, а + с + d+1, d +1), g (a, b, c, d) = (a+1, b, a+c +1, d );

Функция g будет той же, что и в предыдущем случае. Мы уже знаем, что она является функцией четвертого порядка. Вычислим порядок функции f. Для этого применим ее несколько раз, пока не получим тождественное преобразование. Если я не ошибаюсь, достаточно применить ее дважды:

83

f²(а, b, с, d) = f(а+1, b+1, а+с+d+1, d+1)

= ((а+1)+1, (b+1)+1,(a+1) + (a+c+d+1)+(d+1)+1,(d+1)+1)

= (а, b, с, d),

а также использовать упрощения, которые вы продемонстрировали выше.

Более того, f и g независимы, следовательно, порожденная ими группа изоморфна группе ℤ/2 х ℤ/4. Этого достаточно, чтобы доказать: рассматриваемое племя является несократимым, так как в группе ℤ/2 х ℤ/4 недостаточно элементов восьмого порядка для преобразования 16 разновидностей брака между собой.

ВЕЙЛЬ: Поздравляю вас, господин Леви-Стросс! Вы все поняли! В этом случае также можно показать, что общество является сократимым, применив новый, более прямой метод, который я вам сейчас объясню. Рассмотрим брак вида (а, b, с, d). Согласно нашим расчетам, сыновья от этого брака вступят в брак по правилу (a +1,b +1,a + c + cf +1,cf +1).

Важно заметить, что разность между первой и четвертой координатами равна:

(b+1)-(d+1)=b-d.

Точно такой же будет разность между первой и четвертой координатами в исходной разновидности брака! Математики говорят, что эта величина инвариантна относительно f. Более того, она также инвариантна относительно g, так как в этом случае вторая и четвертая координаты не меняются. Следовательно, композиция f и g позволяет получить только те правила, в которых значение b — d равно исходному. К примеру, начав с (1, 1, 1, 0), мы никогда не сможем получить (1, 0, 1, 0), так как в первом случае разность между второй и четвертой координатами равна 1, во втором — 0.

Это означает, что представители клана D2, которые вступают в брак по правилу (I), принадлежат к иной группе, чем представители клана С2, вступающие в брак по той же формуле. Выполнив некоторые действия, мы сможем определить эти две группы в явном виде:

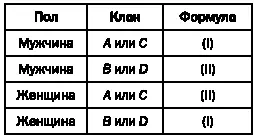
Первая группа.

84

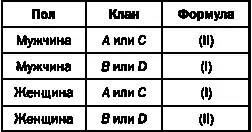
Вторая группа.

ЛЕВИ-СТРОСС: Любой сказал бы, что аборигены мурнгин знали теорию групп.

ВЕЙЛЬ: Когда система, которая на первый взгляд кажется невообразимо сложной, путем умелого выбора обозначений превращается в нечто столь простое, как абелева группа, я воспринимаю это как чудо. Я не осмелюсь сказать, что принцип, согласно которому любой мужчина может жениться на дочери брата своей матери, был введен, чтобы доставить удовольствие математикам (это было бы уже слишком), но следует признать, что я до сих пор испытываю особую привязанность к аборигенам мурнгин.

Видя подобные примеры, сложно не согласиться с сонетом Микеланджело, в котором он говорит, что мраморная глыба уже содержит в себе произведение искусства, и задача художника — отсечь все лишнее:

Математик, подобно великому скульптору, высекает свои творения из необычайно твердого и прочного материала. Несовершенства материала столь сильно влияют на конечный результат, что наделяют его некоторого рода объективностью.

85

ЛЕВИ-СТРОСС: Помните, как в одной из наших бесед вы пообещали мне подробнее рассказать о задаче из вашей докторской диссертации?

ВЕЙЛЬ: Как я мог забыть об этом! Но в этот раз, если вы позволите, мы применим иной метод. Я написал несколько достаточно подробных заметок; прочитайте их, а затем спросите меня о том, что показалось вам непонятным. Вперед!