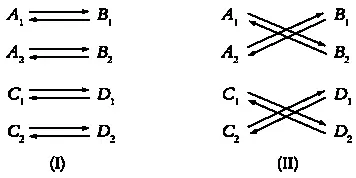Хавьер Фресан - Мир математики - m. 35 Пока алгебра не разлучит нас. Теория групп и ее применение.

Так как h принадлежит группе, для него определен обратный элемент h -1. Припишем h -1с двух сторон равенства и получим h -1(h(M 1)) = h -1(M i). Композицией h и h -1является тождественное преобразование — вспомните определение обратного элемента! Таким образом, Мх = h -1(M i). Это означает, что мы можем получить М 1из M i. Так как правило M 1связано со всеми остальными разновидностями брака, с ними будет связано и любое другое M i. Подгруппы S n, обладающие этим свойством, называются транзитивными. Имеем:

Племя, состоящее из n кланов, является несократимым тогда и только тогда, когда подгруппа S n, порожденная перестановками f и g, является транзитивной.

Объединив это утверждение с предложением 1, получим, что для изучения несократимых обществ, удовлетворяющих трем нашим условиям, необходимо знать: а) какие циклические подгруппы S nтранзитивны и б) какие прямые произведения двух циклических подгрупп S nтранзитивны. Нетрудно видеть, что подгруппа Н

76

группы Sn может быть транзитивной только тогда, когда она содержит по меньшей мере n элементов. Допустим, что эта подгруппа содержит m элементов, где m < n.

Обозначим их через h 1, h 2... h m. С M 1будут связаны следующие разновидности брака: h 1(M 1), h 2(M 2) ... h m(M m). В лучшем случае все они будут различны, однако этот перечень никогда не будет полным, так как он содержит m элементов, а m меньше n. Применив некоторые другие свойства симметрической группы, найти циклические транзитивные подгруппы S nнесложно, однако давайте остановимся на этом — иначе мы никогда не закончим наш разговор о браках!

ЛЕВИ-СТРОСС: Хотя ваши объяснения по сути намного лучше тех, что преддожили первые антропологи, во всех рассмотренных нами примерах они смогли решить поставленную задачу явным перебором всех возможных сочетаний. Теория групп абсолютно необходима тогда, когда число кланов по-настоящему велико или же когда в правилах заключения браков экзогамия сочетается с эндогамией.

Я понял это, едва начав изучать племя аборигенов мурнгин, живущих на севере Австралии, в Арнем-Ленде. Незадолго до того как я начал работу над докторской, один из крупнейших специалистов по австралийским аборигенам Адольфус Петер Элкин указал, что исключительно формальный анализ систем родства у аборигенов не имеет смысла, поскольку никак не помогает узнать обычаи племени.

Но четко изучить структуры родства у аборигенов мурнгин было крайне важно, так как это племя представляло собой одну из немногих систем ограниченного обмена, в которых различались браки между двоюродными братьями и сестрами: брак с дочерью брата матери разрешался, а брак с дочерью сестры отца — нет. Так как ни одна из известных в то время систем не позволяла объяснить это различие, некоторые авторы выбрали более простое решение — они попросту отказались от анализа закономерностей. Но как может столь точное правило, в котором различаются двоюродные братья и сестры и которое является логичным следствием определенной исходной конфигурации, появиться в системе, не подчиняющейся никаким нормам?

Племя мурнгин делится на два сообщества, иритча и дуа, а каждое из них состоит из четырех кланов. Эти кланы называются нгарит, булаин, каийярк, бангарди, бураланг, баланг, кармарунг и вармут. Названия кланов не имеют особого значения — будем обозначать кланы A 1, A 2, B 1, B 2, C 1, C 2, D 1и D 2Сразу же возникает аномалия, характерная для всех племен этого региона: мужчины не всегда обязаны искать себе жену в другом клане. Существуют две альтернативные формулы, (I)

77

и (II). Первая описывает браки внутри одной и той же половины племени, вторая — в разных. Эти формулы представлены на иллюстрации:

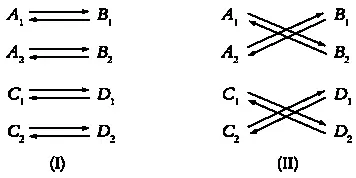
Неизменным остается правило, по которому мать определяет клан своих детей.

Это правило выглядит следующим образом:

ВЕЙЛЬ: Чтобы это общество удовлетворяло нашим условиям, необходимо предположить, что формула, применимая к конкретному человеку, зависит только от его пола и от разновидности брака его родителей, (I) или (II). Для каждого клана определены две разновидности брака, следовательно, имеем 16 различных правил.

Вместо того чтобы обозначить их через М 1, M 2... М 16, введем не совсем обычные обозначения, которые помогут упростить расчеты. Во-первых, поставим в соответствие каждому клану племени тройку из нулей и единиц (а, b, с), где