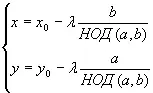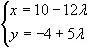Еще одно фундаментальное свойство делимости чисел звучит так: если число а — делитель произведения bс, и нам известно, что а и b — взаимно простые, то а обязательно будет делителем с. В самом деле, в противном случае один из простых делителей а также будет делителем b, и эти числа не будут взаимно простыми.
С другой стороны, если d — наибольший общий делитель а и b, то существуют два целых числа р и q такие, что а = dp, b = dq. Это утверждение выполняется для любых общих делителей, но так как d — НОД, можно утверждать, что р и q взаимно простые — в противном случае а и b имели бы общий делитель, больший d.
Теперь мы знаем все, что нужно для решения диофантовых уравнений вида ах + by = с,
где а, b и c — произвольные целые числа. Чтобы решить это уравнение, нужно найти все пары целых чисел (х, у), которые удовлетворяют соотношению ах + by = с.
Посмотрим, как это сделать. Обозначим через d наибольший общий делитель а и b. По определению а и b делятся на d, следовательно, выражение ах + by также будет делиться на d. Так как согласно исходному уравнению ах + by = с, число d также должно быть делителем с. Следовательно, если с не делится на d, то уравнение не имеет решений. Так, решений не имеет уравнение 50х + 120у = 7. Мы уже показали, что наибольший общий делитель 50 и 120 равен 10, а 7 не делится на 10.
Далее будем предполагать, что с делится на d.
Тогда мы можем записать а = dp, b = dq и с = dr, где р и q — взаимно простые.
Сначала рассмотрим случай с = 0, то есть однородное уравнение ах + by = 0.
91
Разделив на d первый член уравнения, получим следующее: достаточно решить уравнение рх + qy = 0, или, что аналогично, рх = —qy. Будем рассуждать следующим образом: так как рх равно — qy, qy должно делиться на р. Однако р и q взаимно простые, следовательно, остается единственный вариант: у делится на р, то есть существует целое число Λ такое, что у = Λр. Аналогично доказывается, что х делится на q, поэтому существует другое целое число μ такое, что х = μq. Подставив значения х и у в уравнение, получим: μpq = —Λpq, то есть μ = —Λ, так как pq отлично от нуля. Следовательно, решениями уравнения ах + by = 0 будет пара чисел (q, —р) и всех кратных им чисел (Λq, —Λр).
Теперь предположим, что с отлично от нуля. Если известно два решения (x 0, у 0) и (х 1y 1) уравнения ах + by = с, то:
а(х 0- х 1) + b(у 0- у 1) = (ах 0+ by 1-(ax 1+by 1) = с-с = О,
откуда следует, что (x 0— x 1, у 0— y 1) — решение однородного уравнения ах + by = 0.
Так как все решения этого уравнения имеют вид (Λq, —Λр), найдется целое число Λ такое, что x 0— x 1= Λq и у 0— у 1= —Λр, или, что аналогично, х = x 0— Λq и y 1= y 0+Λр. Иными словами, уравнение имеет бесконечно много решений, но все они выводятся из частного решения (x 0, у 0). Напомню, что р и q — результат деления а и b на наибольший общий делитель. Следовательно, мы доказали, что все решения выглядят так:
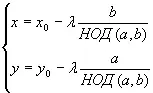
где (x 0, у 0) — частное решение, Λ — любое целое число. Теперь всего лишь осталось найти метод, позволяющий получить (x 0, у 0). Найти эти решения нетрудно, если р и q — взаимно простые, так как по соотношению Безу существуют два целых числа u и v такие, что рu + qv— 1. Умножив u и v на r, получим два числа x 0= ur и у 0= vr такие, что ax 0+ by 0= с.
Рассмотрим пример. Допустим, мы хотим решить диофантово уравнение 50х + 120у = 20.
Мы уже знаем, что наибольший общий делитель 50 и 120 равен 10.
Так как 20 делится на 10, уравнение имеет решение.
92
В этом случае в упрощенном виде уравнение выглядит так: 5х + 12у = 2. Найдем числа, которые мы обозначили через u и v. Так как 1 = 5 — 2 ·2 и 2 = 12 — 2·5, имеем
1 = 5 - 2 · (12 - 2 · 5) = 5 · 5 - 2 · 12,
то есть u = 5, v = —2. Умножив эти значения на 2, получим частное решение (10, —4), на основе которого можно найти общее решение:
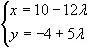
Краткий экскурс в криптографию
Посмотрим, как диофантовы уравнения используются в системе шифрования с открытым ключом. Напомним, что для данного натурального числа n группа целых чисел со сложением по модулю n состоит из элементов [0], [1], [2]...[n — 1], а сложение выполняется следующим образом: сначала мы складываем элементы группы как обычные числа, затем вычитаем n из полученного результата до тех пор, пока не получим число, заключенное на интервале от 0 до n — 1. Аналогично можно определить операцию умножения. Допустим, n = 7 и нам нужно вычислить произведение 4*5. Сначала умножим эти два числа так же, как и целые числа. Получим 20.
Читать дальше