Хавьер Фресан - Мир математики - m. 35 Пока алгебра не разлучит нас. Теория групп и ее применение.

Если, напротив, х = 1, получим y² = 0, то есть у — 0. Подставим в уравнение х = —1.

Правая часть будет равна (—1) 3—2 (—1) + 1 = —1 + 2 + 1 = 2, уравнение примет вид y² = 2. Его решениями будут у = √2 и у = —√2. Таким образом, точки с координатами (—1, √2) и (—1, —√2) также будут лежать на кривой. Эти решения не являются целыми, но это не важно — чтобы изобразить кривую на плоскости, нужно учесть все вещественные решения.

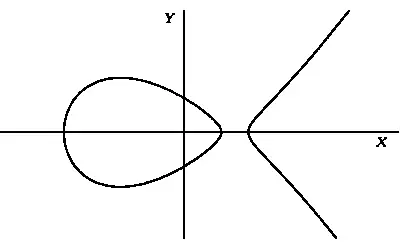
Эллиптическая кривая, заданная уравнением y² = х3-2х + 1.

Теперь выберем две точки Р и Q, лежащие на кривой, и соединим их прямой линией. Будем предполагать, что Р и Q несимметричны относительно оси абсцисс,

98

чтобы соединяющая их прямая не располагалась вертикально. Эта прямая пересечет кривую в точке, которую мы обозначим через PQ. Результатом операции над точками Р и Q будет точка Р + Q, симметричная PQ относительно оси абсцисс.

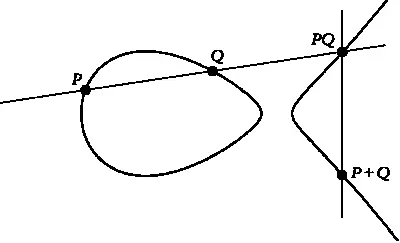
Результат операции сложения для точек P и Q эллиптической кривой.

Необходимо уточнить несколько моментов. Во-первых, прямая, проходящая через точки Р = (x 1, y 1) и Q = (х 2, у 2), пересекает кривую в некоторой третьей точке.

Так как мы предположили, что эта прямая не располагается вертикально, ее уравнение будет иметь вид у = mх + n, где m и n — вещественные числа. Подставив это выражение в уравнение нашей эллиптической кривой, получим:

(mx + n)² = x 3+ax+b.

Путем элементарных преобразований это уравнение можно привести к виду:

х 3-Ах² + Вх + С = 0, (**)

где A = m², В = a — 2mn, С = b — n². Следовательно, теперь нам нужно вычислить корни многочлена третьей степени с вещественными коэффициентами. Два корня уже известны: это абсциссы x 1и х 2точек Р и Q, так как обе эти точки одновременно лежат и на кривой, и на прямой. Используем следующую лемму.

Лемма. Если многочлен третьей степени с вещественными коэффициентами имеет два вещественных корня, то третий корень многочлена также будет вещественным.

99

Докажем лемму. Пусть

Р(х) = x 3+ Rx² + Sx + Т

многочлен третьей степени с вещественными коэффициентами. Обозначим его корни через x 1, х 2, х 3. Следовательно, Р(х) можно представить в виде

Р(х) = (х - x 1) (х - х 2) (х - х 3).

Выразим коэффициенты многочлена через его корни:

Р(х) = x 3— (х 1+x 2+х 3)х² +(x 1x 2+x 1x 3+x 2x 3)х — x 1x 2x 3.

К примеру, — R = x 1+ х 2+ х 3. Чтобы получить третий корень многочлена, нужно вычесть —R из первых двух. По условию, и коэффициент R, и корни x 1и х 2— вещественные числа, следовательно, x 3также будет вещественным числом.

По лемме, которую мы только что доказали, существует вещественное число х 3, которое удовлетворяет уравнению (**).

Подставив это число в равенство у = mx + n, получим координату у 3точки PQ. Осталось найти координаты симметричной ей точки — для этого заменим ординату на противоположную. Результатом операции над точками (x 1, y 1) и (х 2, у 2) будет точка (х 3, —у 3).

Мы показали, что точки Р = (0, 1) и Q = (1, 0) принадлежат эллиптической кривой y² = x 3—2х + 1. Вычислим координаты точки Р + Q. Для этого сначала нужно найти уравнение прямой, проходящей через Р и Q. Несложно показать, что эта прямая задается уравнением у = —х + 1. Получим уравнение:

(—х +1) 2 = x 3—2х +1 ↔ х²—2х + 1 = x 3—2х + 1 ↔ х² = x 3↔ х² (х — 1) = 0.

Решениями этого уравнения будут х = 0 (дважды) и х = 1. Так как x 1= 0 и х 2= 1, искомой точкой будет x 3= 0.

Подставив это значение в уравнение у = —х + 1, получим у = 1.

Таким образом, результатом операции над Р и Q будет точка Р + Q с координатами (0, —1).

Заметим, что в этом случае результатом операции над двумя целочисленными решениями уравнения вновь будет целочисленное решение.

В общем случае это верно тогда, когда коэффициенты уравнения являются целыми числами. Доказательство этого утверждения, по сути, ничем не отличается от доказательства приведенной выше леммы.

Мы преодолели первое препятствие: мы показали, что если прямая проходит через две несимметричные точки эллиптической кривой, то она также пересечет кривую в третьей точке. Но что произойдет, если точки Р и Q симметричны?

100

Они будут иметь координаты Р = (x 1, y 2) и Q = (х 1—у 2), а соединяющая их вертикальная линия будет задаваться уравнением х = х 1Подставив в уравнение эллиптической кривой х = x 1получим у² = х 1 3+ ах 1+b. Мы исключили переменную х и получили, что y² равно вещественному числу. Это уравнение имеет всего два решения, ух и — yv следовательно, прямая, соединяющая Р и Q, не будет пересекать эллиптическую кривую ни в одной другой точке. PQ не существует! Как же справиться с этой проблемой? Решение подскажут художники Возрождения, которые изобрели перспективу. Чтобы сделать свои полотна более реалистичными, они изображали параллельные прямые сходящимися в удаленной точке, называемой точкой схода. Последуем примеру художников и будем считать, что наша вертикальная прямая пересекает эллиптическую кривую в третьей точке О, расположенной на бесконечности. Эта точка будет играть роль точки схода.