dU = δ Q + δ W = δ Q – pdV
dU = δQ v= C VdT = nC VdT
Все количество теплоты, полученное системой, идет на изменение внутренней энергии.
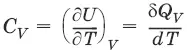
– теплоемкость при постоянном объеме, т. е. количество теплоты, необходимое для повышения температуры системы на один градус при постоянном объеме. [ С V ] = Дж/град.
Ĉ V – мольная теплоемкость при постоянном объеме, Дж/(моль × град). Для идеальных газов:
Ĉ V= 2/ 3R – одноатомный газ;
Ĉ V= 5/ 2R – двухатомный газ.
Изобарный процесс (Р = const)
dU = δ Q + δ W = δQ – pdV
δQ p= dU + pdV = d(U + pV) = dH
H = U + pV – энтальпия – функция состояния системы.
ΔН = Σ(ν iU i) прод– Σ(ν iU i) исх
δQ p= dU + pdV =dH = C pdT – тепловой эффект изобарного процесса равен изменению энтальпии системы.
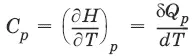
– теплоемкость при постоянном давлении. [ С ] = Дж/град.
Ĉ р – мольная теплоемкость при постоянном давлении, Дж/(моль × град).
Для идеальных газов: Ĉ р= Ĉ V+ R; Ĉ р, Ĉ V= [Дж/(моль • К)].
Тепловой эффект (теплота) химической реакции – количество теплоты, выделившейся либо поглотившейся в ходе реакции при постоянной температуре.
Q v= ΔU V
Q p= ΔU p
Зависимость теплового эффекта реакции от температуры. Закон Кирхгоффа
Температурный коэффициент теплового эффекта химической реакции равен изменению теплоемкости системы в ходе реакции.
Закон Кирхгоффа:
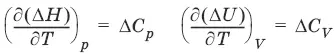
Для химического процесса изменение теплоемкости задается изменением состава системы:
ΔС р = Σ(ν iC p,i) прод– Σ(ν iC p,i) исхили Δ C V= Σ(ν iC V,i) прод– Σ(ν iC V,i) исх
Интегральная форма закона Кирхгоффа:
ΔН Т2= ΔН Т1+ ΔС р(Т 2– T 1 ) или Δ U T2= ΔU Ti+ ΔС V(Т 2– T 1 )
1.3. Второе начало термодинамики. Энтропия
1) Теплота не может самопроизвольно переходить от менее нагретого тела к более нагретому.
2) Невозможен процесс, единственным результатом которого является превращение теплоты в работу.
3) Существует некоторая функция состояния системы, названная энтропией,изменение которой следующим образом связано с поглощаемой теплотой и температурой системы:
в неравновесном процессе
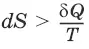
в равновесном процессе
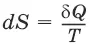
S – энтропия, Дж/град,
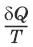
– приведенная теплота.
Статистическая интерпретация энтропии
Каждому состоянию системы приписывается термодинамическая вероятность (определяемая как число микросостояний, составляющих данное макросостояние системы), тем большая, чем более неупорядоченным или неопределенным является это состояние. Энтропия – функция состояния, описывающая степень неупорядоченности системы.
S = k ln W – формула Больцмана.
Система стремится самопроизвольно перейти в состояние с максимальной термодинамической вероятностью.
Расчет абсолютной энтропии
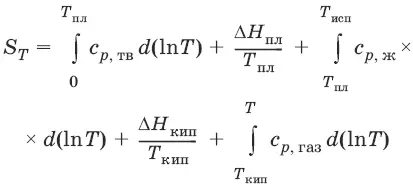
Изменение энтропии в ходе химического процесса определяется только видом и состоянием исходных веществ и продуктов реакции и не зависит от пути реакции:
ΔS = Σ(ν iS i) прод– Σ(ν iS i) исх
Величины абсолютной энтропии в стандартных условиях приведены в справочной литературе.
1.4. Термодинамические потенциалы
Потенциал – величина, убыль которой определяет производимую системой работу.
Самопроизвольно могут протекать только те процессы, которые приводят к понижению свободной энергии системы; система приходит в состояние равновесия, когда свободная энергия достигает минимального значения.
F = U – TS – свободная энергия Гельмгольца – изохорно-изотермический потенциал (Дж) – определяет направление и предел самопроизвольного протекания процесса в закрытой системе, находящейся в изохорно-изотермических условиях.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

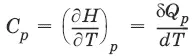
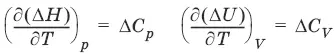
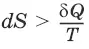
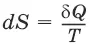
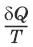
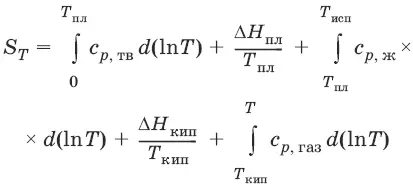







![Кирилл Рябов - Никто не вернётся [сборник litres]](/books/385781/kirill-ryabov-nikto-ne-vernetsya-sbornik-litres-thumb.webp)



