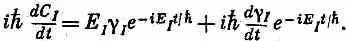
Дифференциальное уравнение обращается в
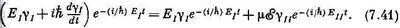
Равным образом уравнение для dC II /dt обращается в
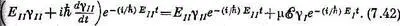
Обратите теперь внимание, что в обеих частях каждого уравнения имеются одинаковые члены. Сократим их и умножим первое уравнение на 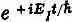
а второе на 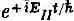
. Вспоминая, что (E I - e ii )=2А=hw 0, мы в конце концов получаем
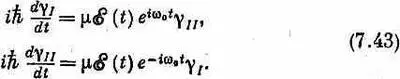
Получилась довольно простая пара уравнений — и пока еще точная. Производная от одной переменной есть функция от времени 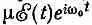 , умноженная на вторую переменную; производная от второй — такая же функция от времени, умноженная на первую. Хотя эти простые уравнения в общем не решаются, но в некоторых частных случаях мы решим их.
, умноженная на вторую переменную; производная от второй — такая же функция от времени, умноженная на первую. Хотя эти простые уравнения в общем не решаются, но в некоторых частных случаях мы решим их.
Нас, по крайней мере сейчас, интересует только случай колеблющегося электрического поля. Взяв x (t) в форме (7.37), мы увидим, что уравнения для g I и g II обратятся в
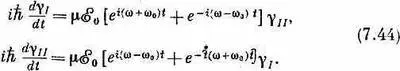
(it
И вот если x 0 достаточно мало, то скорости изменения g I и g II тоже будут малы. Обе у не будут сильно меняться с t, особенно в сравнении с быстрыми вариациями, вызываемыми экспоненциальными членами. У этих экспоненциальных членов есть вещественные и мнимые части, которые колеблются с частотой w+w 0или w-w 0. Члены с частотой w+w 0колеблются вокруг среднего значения (нуля) очень быстро и поэтому не дадут сильного вклада в скорость изменения g. Значит, можно сделать весьма разумное приближение, заменив эти члены их средним значением, т. е. нулем. Их просто убирают и в качестве приближения берут
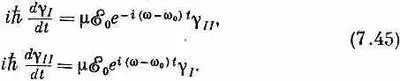
Но даже и оставшиеся члены с показателями, пропорциональными (w-w 0), меняются быстро, если только w не близко к w 0. Только тогда правая сторона будет меняться достаточно медленно для того, чтобы набежало большое число, пока интегрируешь эти уравнения по t. Иными словами, при слабом электрическом поле изо всех частот представляют важность лишь те, которые близки к w 0.
При тех приближениях, которые были сделаны для того, чтобы получить (7.45), эти уравнения можно решить и точно; но работа эта все же трудоемкая, и мы отложим ее на другое время, когда обратимся к другой задаче того же типа. Пока же мы их просто решим приближенно, или, лучше сказать, найдем точное решение для случая идеального резонанса w=w 0и приближенное — для частот близ резонанса.
§ 4. Нереходы при резонансе
Первым рассмотрим случай идеального резонанса. Если положить w=w 0, то экспоненты в обоих уравнениях (7.45) станут равными единице, и мы просто получим
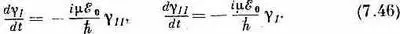
Если из этих уравнений исключить сперва g I , а потом g II , то мы увидим, что каждое из них удовлетворяет дифференциальному уравнению простого гармонического движения

Общее решение этих уравнений может быть составлено из синусов и косинусов. Легко проверить, что решениями являются следующие выражения:
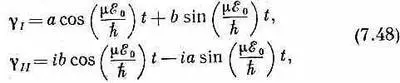
где а и b — константы, которые надо еще определить так, чтобы они укладывались в ту или иную физическую ситуацию.
К примеру, предположим, что при t =0 наша молекулярная система была в верхнем энергетическом состоянии | I >, а это требует [из уравнения (7.40)], чтобы g I =1 и g II =0 при t =0. Для такого случая должно быть а =1 и b =0. Вероятность того, что молекула окажется в том же состоянии | I > в какой-то позднейший момент t, равна квадрату модуля g I , или
Читать дальше

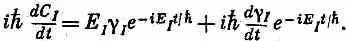
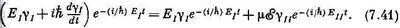
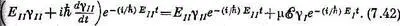
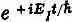
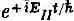
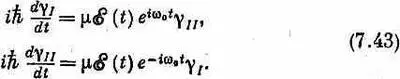
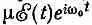 , умноженная на вторую переменную; производная от второй — такая же функция от времени, умноженная на первую. Хотя эти простые уравнения в общем не решаются, но в некоторых частных случаях мы решим их.
, умноженная на вторую переменную; производная от второй — такая же функция от времени, умноженная на первую. Хотя эти простые уравнения в общем не решаются, но в некоторых частных случаях мы решим их.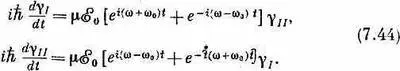
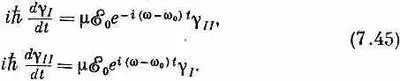
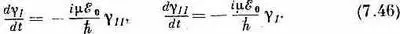

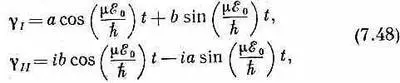



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)

![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


