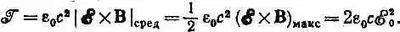
(Максимум x равен 2x 0.) Вероятность перехода принимает вид
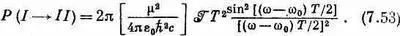
Обычно свет, освещающий подобную систему, не точно монохроматичен. Поэтому интересно решить еще одну задачу— подсчитать вероятность перехода, когда интенсивность света на единицу интервала частот равна 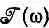 и покрывает собой широкую полосу, включающую w 0. Тогда вероятность перехода от | I > к | II > обратится в интеграл
и покрывает собой широкую полосу, включающую w 0. Тогда вероятность перехода от | I > к | II > обратится в интеграл
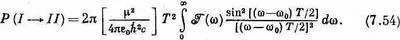
Как правило, 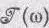 меняется с w медленнее, чем острый резонансный фактор. Эти две функции могут выглядеть так, как показано на фиг. 7.8.
меняется с w медленнее, чем острый резонансный фактор. Эти две функции могут выглядеть так, как показано на фиг. 7.8.
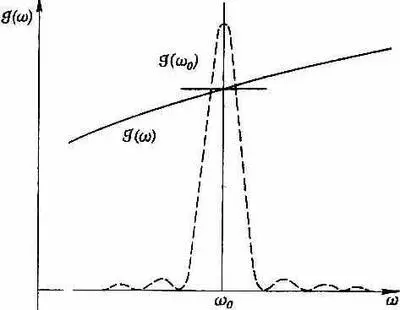
Фиг. 7.8. Спектральная интенсивность 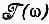 может быть представлена своим значением при w 0 .
может быть представлена своим значением при w 0 .
В таких случаях можно заменить 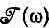 ее значением
ее значением 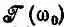 в центре острой резонансной кривой и вынести из-под интеграла. Оставшийся интеграл — это просто площадь под кривой на фиг. 7.7, которая, как известно, равна 2p/Т. Мы приходим к результату
в центре острой резонансной кривой и вынести из-под интеграла. Оставшийся интеграл — это просто площадь под кривой на фиг. 7.7, которая, как известно, равна 2p/Т. Мы приходим к результату
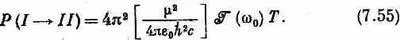
Это очень важный результат; перед нами общая теория поглощения света любой молекулярной или атомной системой. Хотя мы вначале считали, что состояние | I > обладает более высокой энергией, чем состояние | II >, но никакие наши рассуждения от этого не зависели. Уравнение (7.55) соблюдается и тогда, когда энергия состояния | I > ниже энергии состояния | II >; тогда Р (I®II) представляет собой вероятность перехода с поглощением энергии от падающей электромагнитной волны. Поглощение атомной системой света всегда предполагает, что имеется амплитуда для перехода в колеблющемся электрическом поле между состояниями, отличающимися на энергию E = hw 0. В каждом отдельном случае она рассчитывается так же, как мы это проделали, и дает выражения наподобие (7.55). Поэтому мы подчеркнем следующие свойства этой формулы. Во-первых, вероятность пропорциональна Т. Иными словами, существует неизменная вероятность на единицу времени, что переход произойдет. Во-вторых, эта вероятность пропорциональна интенсивности света, падающего на систему. В-третьих, вероятность перехода пропорциональна m 2, где, как вы помните, m x определяет энергетический сдвиг, вызываемый электрическим полем x. По этой именно причине m x появлялось и в уравнениях (7.38) и (7.39) в качестве коэффициента связи, ответственного за переход между стационарными состояниями | I > и | II >. Иными словами, для рассматривавшихся нами малых x член m x есть так называемое «возмущение» в матричном элементе гамильтониана, связывающем состояния |/> и |//>. В общем случае m x заменилось бы матричным элементом < II | H | I > (см. гл. 3, § 6).
В гл. 42, § 5 (вып. 4) мы говорили о связи между поглощением света, вынужденным испусканием и самопроизвольным испусканием в терминах введенных Эйнштейном коэффициентов А и В. Здесь наконец-то в наших руках появляется квантовомеханическая процедура для подсчета этих коэффициентов. То, что мы обозначили Р ( I ® II ) для нашей аммиачной двухуровневой молекулы, в точности соответствует коэффициенту поглощения B nm в эйнштейновской теории излучения. Из-за сложности молекулы аммиака — слишком трудной для расчета — нам пришлось взять матричный элемент < II|H | I > в виде m x и говорить, что m извлекается из опыта. Для более простых атомных систем величину m mn , отвечающую к произвольному переходу, можно подсчитать, исходя из определения
Читать дальше

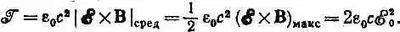
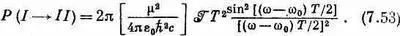
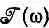 и покрывает собой широкую полосу, включающую w 0. Тогда вероятность перехода от | I > к | II > обратится в интеграл
и покрывает собой широкую полосу, включающую w 0. Тогда вероятность перехода от | I > к | II > обратится в интеграл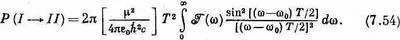
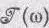 меняется с w медленнее, чем острый резонансный фактор. Эти две функции могут выглядеть так, как показано на фиг. 7.8.
меняется с w медленнее, чем острый резонансный фактор. Эти две функции могут выглядеть так, как показано на фиг. 7.8.
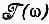 может быть представлена своим значением при w 0 .
может быть представлена своим значением при w 0 .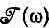 ее значением
ее значением 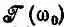 в центре острой резонансной кривой и вынести из-под интеграла. Оставшийся интеграл — это просто площадь под кривой на фиг. 7.7, которая, как известно, равна 2p/Т. Мы приходим к результату
в центре острой резонансной кривой и вынести из-под интеграла. Оставшийся интеграл — это просто площадь под кривой на фиг. 7.7, которая, как известно, равна 2p/Т. Мы приходим к результату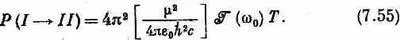



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)

![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


