У гамильтониана есть одно свойство, которое выводится сразу же:
Н* ij =H ji . (6.40)
Это следует из того, что полная вероятность пребывания системы хоть в каком-то состоянии не должна меняться. Если вначале у вас была частица (или любой объект, или весь мир), то с течением, времени она пропасть не может. Полная вероятность ее где-то найти равна
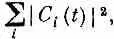
что не должно меняться со временем. Если это обязано выполняться для любого начального условия j, то уравнение (6.40) тоже должно соблюдаться.
В качестве первого примера возьмем случай, когда физические условия не меняются со временем; мы имеем в виду внешние физические условия, так что Н не зависит от времени никаких магнитов никто не включает и не выключает. Выберем также систему, для описания которой хватает одного базисного состояния; такое приближение годится для покоящегося атома водорода и сходных систем. Уравнение (6.39) тогда утверждает, что

Только одно уравнение — и все! Если Н 11постоянно, это дифференциальное уравнение легко решается, давая
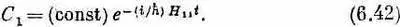
Так зависит от времени состояние с определенной энергией Е=Н 11 . Вы видите, почему Н ij следовало бы называть энергетической матрицей: она обобщает понятие энергии на более сложные случаи.
Вслед за этим, чтобы еще лучше разобраться в смысле уравнений, рассмотрим систему с двумя базисными состояниями.
Тогда (6.39) читается так:
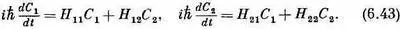
Если все Н опять не зависят от времени, то эти уравнения легко решить. Для интереса займитесь этим сами, а мы позже еще вернемся к ним. Вот вы уже и можете вести расчеты по квантовой механике, зная об Н только то, что оно не зависит от времени!
§ 6. Молекула аммиака
Теперь мы хотим продемонстрировать, как динамическое уравнение квантовой механики может быть использовано для описания какой-то физической обстановки. Мы выбрали интересный и простой пример, в котором, сделав некоторые разумные предположения о гамильтониане, сможем вывести кое-какие важные (и даже практически важные) результаты. Возьмем случай, когда достаточно двух состояний,— это молекула аммиака.
Молекулу аммиака образуют один атом азота и три атома водорода, плоскость которых проходит мимо атома азота, так что молекула имеет форму пирамидки (фиг. 6.1, а).
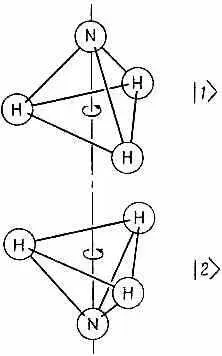
Фиг. 6.I. Два равноценных геометрических расположения молекулы аммиака.
Эта молекула, как и всякая другая, обладает бесконечным количеством состояний. Она может вращаться вокруг какой угодно оси; двигаться в любом направлении, вибрировать и т. д. и т. п. Значит, это вовсе не система с двумя состояниями. Но мы сделаем следующее приближение: предположим, что все прочие степени свободы закреплены и не связаны с теми, которые нас сейчас интересуют. Будем считать, что молекула может только вращаться вокруг оси симметрии (как показано на рисунке), что импульс ее переносного движения равен нулю и что ее колебания очень слабы. Это фиксирует все условия, кроме одного: для, атома азота все еще существуют два возможных положения — он может оказаться по одну сторону плоскости атомов водорода, а может оказаться и по другую (фиг. 6.1). Так что мы будем рассуждать о молекуле, как если бы она была системой с двумя состояниями. Под этим подразумевается, что существуют только два состояния, о которых реально следует заботиться, все же прочее предполагается зафиксированным. Как видите, если даже известно, что молекула вращается вокруг оси с определенным моментом количества движения и что она движется с определенным импульсом и колеблется определенным образом, то все равно еще остаются два Допустимых состояния. Будем говорить, что молекула находится в состоянии |1>, когда азот «вверху» (фиг. 6.1, а) и в состоянии |2>, когда азот «внизу» (фиг. 6.1, б). Состояния | 1 > и | 2 > в нашем анализе поведения молекулы аммиака можно принять за совокупность базисных состояний В каждый момент истинное состояние |y> молекулы может быть представлено заданием C 1=<1|y> — амплитуды пребывания в состоянии \1 и С 2=<2|y> — амплитуды пребывания в состоянии |2>. Тогда, используя (6.8), вектор состояния |y> можно записать так:
Читать дальше

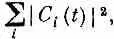

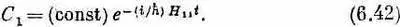




![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)

![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


