Нам пока мало известно об U ij . Мы знаем только, что при D t, стремящемся к нулю, ничего не должно произойти, просто должно получиться начальное состояние. Значит, U ij ®1 и U ij ®0 при i№j. Иными словами, U ij ® d ij при D t ®0. Кроме того, мы вполне вправе предположить, что при малых At каждый из U ij обязан отличаться от d ij на величину, пропорциональную D t; так что можно писать

Однако обычно по историческим и по иным причинам из коэффициентов К ij выносят множитель
(- i/h) ; предпочитают писать
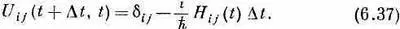
Это, разумеется, то же самое, что и (6.36). Если угодно, это просто определение коэффициентов H ij ( t ).Члены H ij — это как раз производные по t 2от коэффициентов U ij ( t 2 , t 1) , вычисляемые при t 2 =t 1 =t,
Подставляя в (6.35) этот вид U , получаем
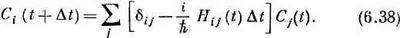
Суммируя члены с d ij , получаем просто C i ( t ) , что можно перенести в другую сторону уравнения. После деления на D t мы распознаем в этом производную
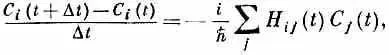
или
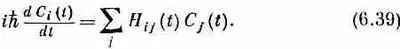
Вы помните, что С i ( t ) — это амплитуда < i| y> обнаружить состояние y в одном из базисных состояний i (в момент t). Значит, уравнение (6.39) сообщает нам, как каждый из коэффициентов < i| y> меняется со временем. Но это все равно, что сказать, что (6.39) сообщает нам, как со временем меняется состояние y, раз мы описываем y через амплитуды < i |y>. Изменение y со временем описывается через матрицу Н ij , которая, конечно, должна включать все то, что мы делали с системой, чтобы вызвать ее изменения. Если мы знаем матрицу H ij , которая содержит в себе всю физику явления и может, вообще говоря, зависеть от времени, то у нас есть полное описание поведения системы во времени. Таким образом, (6.39)— это квантовомеханический закон для динамики мира.
(Нужно сказать, что мы всегда будем выбирать совокупность базисных состояний, которые фиксированы и со временем не меняются. Иногда используют такие базисные состояния, которые сами меняются. Однако это все равно, что пользоваться в механике вращающейся системой координат, а мы не хотим входить в подобные тонкости.)
§ 5. Гамилътонова матрица
Идея, стало быть, заключается в том, что для квантовомеханического описания мира нужно выбрать совокупность базисных состояний i и написать физические законы, задавая матрицу коэффициентов Н ij . Тогда у нас будет все, что нужно,— мы сможем отвечать на любой вопрос о том, что случится. Нам остается выучить правила, по которым находят Н в соответствии с данной физической обстановкой: какое Н отвечает магнитному полю, какое электрическому и т. д. Это самая трудная часть дела. К примеру, для новых странных частиц мы совершенно не представляем, какие Н ij употреблять. Иными словами, никто не знает полного H ij для всего мира. (Частично трудность заключается в том, что едва ли можно надеяться на открытие Н ij , раз никому не известно, каковы базисные состояния!) Мы действительно владеем превосходными приближениями для нерелятивистских явлений и некоторых других особых случаев. В частности, мы знаем вид Н ij , требуемый для движений электронов в атомах — для описания химии. Но мы не знаем полного, истинного Н для всей Вселенной.
Коэффициенты H ij называют гамильтоновой матрицей, или, короче, просто гамильтонианом. (Как получилось, что Гамильтон, работавший в 30-х годах прошлого века, дал свое имя квантовомеханической матрице,— история длинная.) Много лучше было бы называть ее энергетической матрицей по при чинам, которые станут ясны, когда мы поработаем с ней. Итак все сошлось на гамильтониане. Как узнать гамильтониан — вот в чем вопрос!
Читать дальше


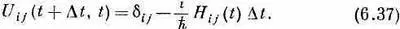
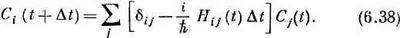
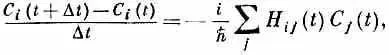
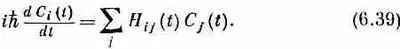



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)

![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


