S |j>.
Или, если пользоваться формой (6.28), ему нужно вычислить матрицу
| S | j>,
называемую S-матрицей. Стало быть, если вы увидите физика-теоретика, который меряет шагами комнату и говорит: «Мне нужно только вычислить S -матрицу», — то вы теперь уже будете понимать, над чем он ломает голову.
Как анализировать S-матрицу, т. е. как указать законы для нее,— вопрос интересный. В релятивистской квантовой механике при высоких энергиях это делается одним способом, в нерелятивистской же квантовой механике — другим, более удобным. (Он годится и в релятивистском случае, но перестает быть таким удобным.) Состоит он в том, чтобы вывести U -матрицу для небольших интервалов времени, т. е. для близких t 2и t 1. Если мы сможем найти последовательность таких U для последовательных интервалов времени, то сможем проследить за тем, как все меняется в зависимости от времени. Сразу же ясно, что для теории относительности этот способ не очень хорош, потому что не так уж просто указать, как «одновременно» все всюду выглядит. Но не стоит нам думать об этом; нашей заботой будет только нерелятивистская механика.
Рассмотрим матрицу U для задержки от t 1до t 3 , где t 3больше t 2 . Иными словами, возьмем три последовательных момента: t 1меньше t 2, t 2меньше t 3 . Тогда мы утверждаем, что матрица, которая тянется от t 1до t 3 , получается перемножением подряд всего того, что происходит при задержке от t 1до t 2 , и затем от t 2до t 3 . Это в точности то же самое, что было с двумя последовательными приборами В и А. Тогда, следуя обозначениям, принятым в гл. 3, § 6, мы можем написать
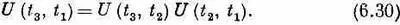
Иначе говоря, можно проанализировать любой интервал времени, если мы умеем анализировать последовательность промежуточных коротких интервалов. Мы просто перемножаем все куски; это и есть способ нерелятивистского анализа квантовой механики.
Итак, задача состоит в том, чтобы узнать матрицу U ( t 2 , t 1) для бесконечно малого интервала времени — для t 2= t 1+D t . Спросим себя: если сейчас у нас есть состояние j, то как оно будет выглядеть через бесконечно малое время D t ? Посмотрим, как это можно расписать. Обозначим состояние в момент t через |y( t )> (мы указываем зависимость y от времени, чтобы было совершенно ясно, что речь идет об условиях в момент t). Теперь зададим вопрос: каково будет положение вещей через короткое время D t ? Ответ таков:
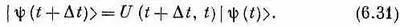
Здесь имеется в виду то же, что и в (6.25), а именно, что амплитуда обнаружить c в момент t+ D t есть
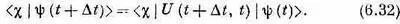
Поскольку мы еще не очень хорошо разбираемся в этих абстрактных вещах, то давайте спроецируем наши амплитуды в определенное представление. Умножая обе части (6.31) на < i |, получаем
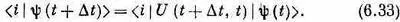
Можно также разложить и |y(t)> на базисные состояния и написать
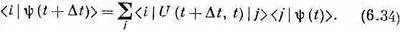
Понять это можно так. Если через C i (t)= < i| y|( t )> обозначить амплитуду пребывания в базисном состоянии i в момент t, то можно считать эту амплитуду (помните, это просто число !) меняющейся во времени. Каждое С i становится функцией времени t. Кроме того, у нас есть информация о том, как амплитуды С i меняются во времени. Каждая амплитуда в момент (t+ D t) пропорциональна всем прочим амплитудам в момент t, умноженным на ряд коэффициентов. Обозначим U -матрицу через U ij , считая, что
U ij = > .
Тогда (6.34) можно записать так:
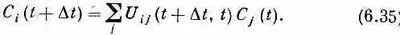
Вот как будет выглядеть динамика квантовой механики.
Читать дальше

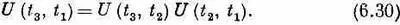
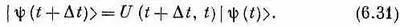
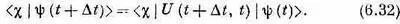
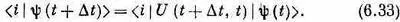
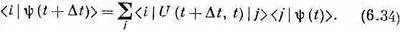
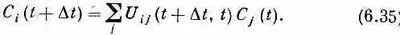



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)

![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


