k y/k =sinq i, k y/k"=sinq t. (33.46)
Но ввиду уравнения (33.44) мы получаем
n 2sinq t =n i sinq i ;, (33.47)
т. е. уже известный нам закон Снелла для преломления. Если же показатель преломления не вещественный, то волновые числа оказываются комплексными и нам следует воспользоваться
(33.45). [Конечно, мы могли бы определить углы q i. и q tиз
(33.46), и тогда закон Снелла (33.47) был бы верен и в общем случае. Однако при этом углы тоже стали бы комплексными числами и, следовательно, потеряли бы свою геометрическую интерпретацию как углы. Уж лучше описывать поведение волн соответствующими комплексными величинами k xили k" x .. ]
До сих пор мы не обнаружили ничего нового. Мы доставили себе только простенькое развлечение, выводя очевидные вещи из сложного математического механизма. А сейчас мы готовы найти амплитуды волн, которые нам еще не известны. Используя результаты для всех w и k, мы можем сократить экспоненциальный множитель в (33.38) и получить
е 0 +е' 0 =е" 0 . (33.48)
Но поскольку мы не знаем ни Е' 0 , ни Е" 9 , то необходимо еще одно соотношение. Нужно использовать еще одно граничное условие. Уравнения для Е х и Е y не помогут, ибо все Еимеют только одну z-компоненту. Так что мы должны воспользоваться условием на В. Попробуем взять (33.29):
B x2=B x1. Согласно условиям (33.35)—(33.37),
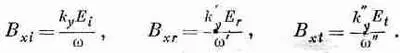
Вспоминая, что w" =w'= w и k" y =k' y =k y , получаем
е 0 +е' 0 =е" 0 .
Но это снова уравнение (33.48)! Мы напрасно потратили время и получили то, что уже давно нам известно.
Можно было бы обратиться к (33.30) B z 2 =В z 1 , но у вектора В отсутствует z-компонента! Осталось только одно условие — (33.31) В у 2 =В у1 . Для наших трех волн
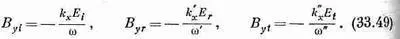
Подставляя вместо E i ,E r и E t волновые выражения при x=0 (ибо дело происходит на границе), мы получаем следующее граничное условие:
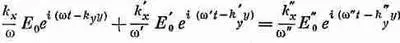
Учитывая равенство всех w и k y , снова приходим к условию k x E 0 + k' x E' 0 =k" x E" 0 . (33.50)
Это дает нам уравнение для величины Е, отличное от (33.48). Получившиеся два уравнения можно решить относительно E' 0и Е" 0 . Вспоминая, что k’ x=- k x , получаем
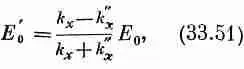

Вместе с (33.45) или (33.46) для k” x эти формулы дают нам все, что мы хотели узнать. Следствия полученного результата мы обсудим в следующем параграфе.
Если взять поляризованную волну с вектором Е, параллельным плоскости падения, то Е, как это видно из фиг. 33.7, будет иметь как x-, так и y-компоненту. Вся алгебра при этом будет менее хитрая, но более сложная. (Можно, правда, несколько уменьшить работу в этом случае, выражая все через магнитное поле, которое целиком направлено по оси z.)
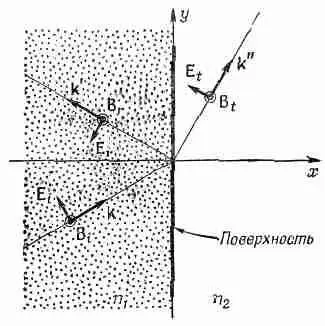
Фиг. 33.7. Поляризации волн, когда поле Е в падающей волне параллельно плоскости падения.
При этом мы найдем
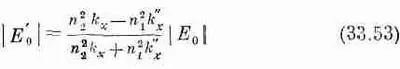
и
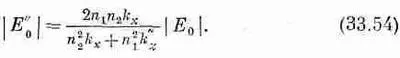
Давайте посмотрим, будет ли наш результат согласовываться с тем, что мы получали раньше. Выражение (33.3) мы вывели в вып. 3, когда находили отношение интенсивностей отраженной и падающей волн. Однако тогда мы рассматривали только вещественный показатель преломления. Для вещественного показателя (или вещественных k) можно записать:
Читать дальше

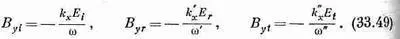
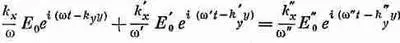
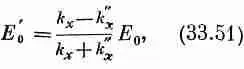


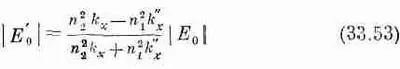
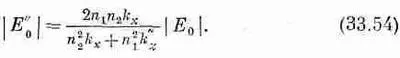



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
