Для нашей прямоугольной петли можно показать, что U мехсоответствует также работе, затрачиваемой на то, чтобы внести петлю в поле. Полная сила, действующая на петлю, равна нулю лишь в однородном поле, а в неоднородном все равно останутся какие-то силы, действующие на токовую петлю. Внося петлю в поле, мы вынуждены будем пронести ее через места, где поле неоднородно, и там будет затрачена работа. Будем считать для упрощения, что петлю вносят в поле так, что ее момент направлен вдоль поля. (А в конце, уже в поле, ее можно повернуть как надо.)
Вообразите, что мы хотим двигать петлю в направлении x, т. е. в ту область, где поле сильнее, и что петля ориентирована так, как показано на фиг. 15.2. Мы отправимся оттуда, где поле равно нулю, и будем интегрировать силу по расстоянию по мере того, как петля входит в поле.
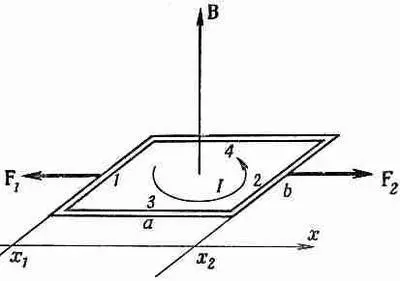
Фиг. 15.2. Петлю проносят через поле В (поперек него) в направлении x.
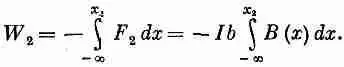
Рассчитаем сначала работу переноса каждой стороны по отдельности, а затем все сложим (вместо того, чтобы складывать силы до интегрирования). Силы, действующие на стороны 3 и 4, направлены поперек движения, так что на эти стороны работа не тратится. Сила, действующая на сторону 2, направлена по x и равна 1bВ(x); чтобы узнать всю работу против действия магнитных сил, нужно проинтегрировать это выражение по x от некоторого значения х, где поле равно нулю, скажем, от х = -Ґ до теперешнего положения х 2 :
(15.6)
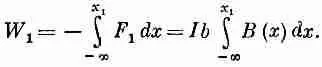
Подобно этому, и работа против сил, действующих на сторону 1 ,равна
(15.7)
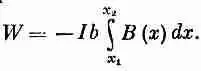
Чтобы вычислить каждый интеграл, надо знать, как В(х) зависит от х. Но ведь сторона 1 при движении рамки расположена все время параллельно стороне 2 на одном и том же расстоянии от нее, так что в ее интеграл входит почти вся работа, затраченная на перемещение стороны 2. Сумма (15.6) и (15.7) на самом деле равна
(15.8)
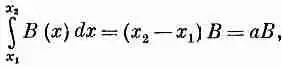
Но, попав в область, где В на обеих сторонах 1 и 2 почти одинаково, мы имеем право записать интеграл в виде
где В — поле в центре петли. Вся вложенная механическая энергия оказывается равной
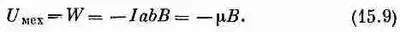
Это согласуется с выражением для энергии (15.4), выбранным нами прежде.
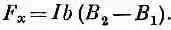
Конечно, тот же вывод получился бы, если бы мы до интегрирования сложили все силы, действующие на петлю. Если бы мы обозначили через В 1 поле у стороны 1 а через В 2 — поле у стороны 2, то вся сила, действующая в направлении х, оказалась бы равной
Если петля «узкая», т. е. если В 2 и В 1 не очень различаются между собой, то можно было бы написать
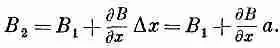
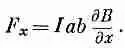
Так что сила была бы равна
(15.10)
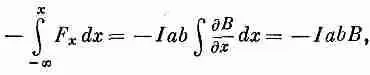
Вся работа, произведенная внешними силами над петлей, равнялась бы
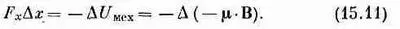
а это опять - mB. Но теперь нам становится понятно, почему получается, что сила, действующая на небольшую токовую петлю, пропорциональна производной магнитного поля, как это следовало ожидать из
Другой наш результат состоит в следующем. Хоть и не исключено, что не все виды энергии вошли в формулу U мех= m·B (ведь это просто некоторая имитация энергии), ею все же можно пользоваться, применяя принцип виртуальной работы, чтобы узнать, какие силы действуют на петли с постоянным током.
§ 2. Механическая и электрическая энергии
Читать дальше


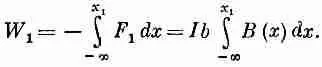
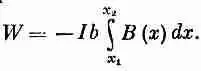
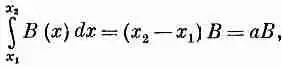
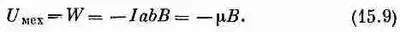
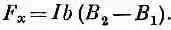
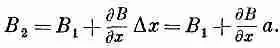
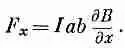
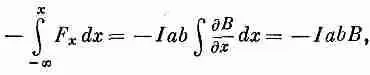
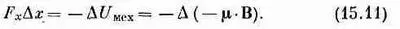



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
