Ричард Фейнман - 4. Кинетика. Теплота. Звук

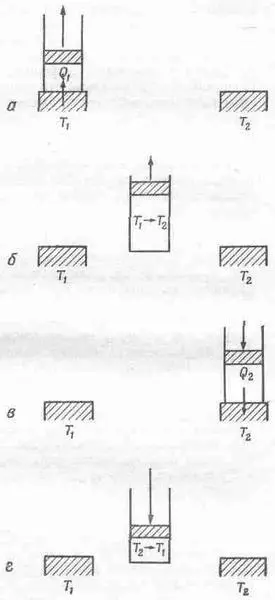
Фиг. 44.5. Шаги цикла Карно.

а — шаг 1. Изотермическое расшире­ния при t 1 , поглощается тепло Q 1; 6 — шаг 2. Адиабатическое расшире­ние; температура падает от T 1 , до Т 2 ; в — шаг 3. Изотермическое сжа­тие при Т 2; выделяется тепло Q 2 ; г —шаг 4. Адиабатическое сжатие; температура поднимается от Т 2 , до T 1 .

Будем считать, что Т 1 больше Т 2 . Для начала нагреем газ и, положив цилиндр на подушку T 1, позволим газу расшириться. Пусть по мере притока тепла в газ поршень очень медленно выдвигается из цилиндра. Тогда можно поручиться, что темпе­ратура газа не будет сильно отклоняться от Т 1 . Если выдер­нуть поршень очень быстро, температура в цилиндре может упасть значительно ниже Т 1 и процесс уже нельзя будет счи­тать полностью обратимым. Если же мы будем медленно вы­таскивать поршень, температура газа останется близкой к температуре Т 1 . С другой стороны, если поршень медленно вдвигать обратно в цилиндр, температура станет лишь чуть-чуть повыше температуры Т 1 и тепло потечет вспять. Вы видите, что такое изотермическое (при постоянной температуре) рас­ширение может быть обратимым процессом, если только произ­водить его медленно и осторожно.

Чтобы лучше понять, что происходит, нарисуем кривую зависимости давления газа от его объема (фиг. 44.6).

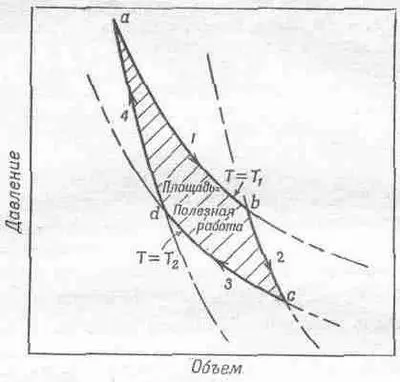
Фиг. 44.6. Цикл Карно.

Когда газ расширяется, его давление падает. Кривая 1 показывает, как изменяются объем и давление, если в цилиндре поддер­живается постоянная температура Т 1 . Для идеального газа эта кривая описывается уравнением PV=NkT 1 . Во время изотер­мического расширения по мере увеличения объема давление падает, пока мы не остановимся в точке b . За это время газ заберет из резервуара тепло Q 1 , ведь мы уже знаем, что если бы газ расширялся, не соприкасаясь с резервуаром, он бы остыл. Итак, мы закончили расширение в точке b. Давайте теперь: снимем цилиндр с резервуара и продолжим расширение.

Но теперь теплу уже неоткуда взяться. И снова мы медленно выдвигаем поршень, так что нет причины, почему бы процесс мог быть необратимым. Конечно, мы опять предполагаем, что трения нет. Газ продолжает расширяться, и температура па­дает, потому что связь с источниками тепла прервана.

Будем расширять газ так, чтобы расширение описывалось кривой 2 до тех пор, пока мы не достигнем точки с, где температура упадет до T 2 . Такое расширение без притока тепла называется адиабатическим. Мы уже знаем, что в случае иде­ального газа кривая 2 имеет вид PV g=const, где g — постоян­ная, большая единицы; поэтому адиабатическая кривая падает круче изотермической. Если температура газа в цилиндре

достигла Т 2 , то, положив цилиндр на вторую тепловую подушку, мы не рискуем вызвать температурных изменений.

Теперь можно медленно сжать газ, продвигаясь по кривой 3, причем цилиндр соприкасается с резервуаром при температуре t 2 (см. фиг. 44.5, шаг 2). Поскольку цилиндр соприкасается с резервуаром, его температура не может повыситься, но газу придется отдать резервуару тепло Q 2 при температуре T 2 . Продвинувшись по кривой 3 до точки d, мы снова снимем цилиндр с тепловой подушки при температуре Т 2 и продолжаем сжимать газ. На этот раз мы не станем отбирать у газа тепло. При этом поднимется температура, а давление пойдет по кривой 4. Если мы тщательно проделаем все этапы, то вернемся к исходной точке а при температуре Т 1 иможем повторить цикл. По этой диаграмме судя, газ совершил полный цикл, отняв за это время тепло Q 1 при температуре T 1и отдав тепло Q 2нри температуре T 2. Этот цикл обратим, и поэтому мы можем шаг за шагом проделать весь путь в обратном направлении. Мы могли бы пойти назад, а не вперед, могли бы начать движение из точки а при температуре T 1, двигаться по кривой 4, затем поглотить тепло Q 2при температуре T 2(для этого надо все время выдвигать поршень) и т. д., пока цикл не будет завершен. Если мы совершали цикл в одном направлении, то заставили газ работать, если же нам захотелось повернуть назад, то придется поработать самим.