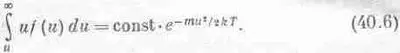
Полное число молекул, проходящих через поверхность за время t, равно числу молекул, способных достигнуть поверхности, а это молекулы, проходящие к поверхности с расстояния ut. Таким образом, число молекул, достигающих площадки, определяется не просто числом молекул, движущихся с данной скоростью, а равно этому числу, отнесенному к единице объема, и умноженному на расстояние, которое они пройдут, прежде чем достигнут площадки, сквозь которую они, по-видимому, должны пройти, а это расстояние пропорционально и. Значит, нам предстоит вычислить интеграл от произведения и на f(u)du, взятый от и до бесконечности, причем мы уже знаем, что этот интеграл обязательно должен быть пропорционален ехр(- mu 2 /2kT), а постоянную пропорциональности еще надо определить:
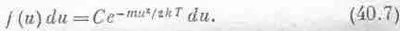
Если теперь продифференцировать интеграл по и, то мы получим подынтегральное выражение (со знаком минус, потому что и — это нижний предел интегрирования), а дифференцируя правую часть равенства, мы получим произведение и на экспоненту (и на некоторую постоянную). Сократим в обеих частях и, и тогда
Мы оставили в обеих частях равенства du, чтобы помнить, что это распределение; оно говорит нам об относительном числе молекул, имеющих скорость между u и u+du .
Постоянная С должна определиться из условия равенства интеграла единице в согласии с уравнением (40.5). Можно доказать, что
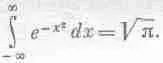
Используя это обстоятельство, легко найти С=Ц(m/2pkT).
Поскольку скорость и импульс пропорциональны, можно утверждать, что распределение молекул по импульсам, отнесенное к единице импульсной шкалы, также пропорционально ехр(- к.э./kT). Оказывается, что эта теорема верна также в теории относительности, если только формулировать ее в терминах импульсов, тогда как в терминах скоростей это уже не так; поэтому сформулируем все в терминах импульсов:
f(p)dp=ce - к.э. / kT dp. (40.8)
Это значит, что мы установили, что вероятности, определяемые энергиями разного происхождения (и кинетической и потенциальной), в обоих случаях выражаются одинаково: ехр(-энергия/kT); таким образом, наша замечательная теорема приобрела форму, весьма удобную для запоминания.
Однако пока мы говорили только о «вертикальном» распределении скоростей. Но мы можем спросить, какова вероятность того, что молекула движется в другую сторону? Конечно, эти распределения связаны друг с другом и можно получить полное распределение, исходя из какого-то одного, ведь полное распределение зависит только от квадрата величины скорости, а не от ее z-составляющей. Распределение по скоростям не должно зависеть от направления и определяться только функцией u 2— вероятностью величины скорости. Нам известно распределение z-составляющей, и мы хотим получить отсюда распределение других составляющих. В результате полное распределение по-прежнему пропорционально ехр(-к.э./kT), только теперь кинетическая энергия состоит из трех частей: mv 2 x /2, mv 2 y /2 и mv 2 z /2, суммируемых в показателе экспоненты. А можно записать это и в виде произведения:
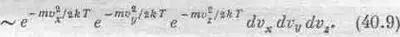
f(v x ,, v y , v z ) dv x dv y dv z ~
Вы можете убедиться в том, что эта формула верна, ибо, во-первых, распределение зависит только от v 2и, во-вторых, вероятности данных v г получаются после интегрирования по всем v x и v yи это должно привести к (40.7). Но обоим этим требованиям удовлетворяет только функция (40.9).
§ 5. Удельные теплоемкости газов
Посмотрим теперь, как можно проверить теорию и оценить, насколько хороша классическая теория газов. Мы уже говорили, что если U— внутренняя энергия N молекул, то формула pV=NkT =(g-1) U иногда и для некоторых газов может оказаться правильной. Мы знаем, что для одноатомного газа правая часть равна 2/ 3кинетической энергии движения центров масс атомов. В случае одноатомного газа кинетическая энергия равна внутренней энергии, поэтому g-1 == 2/з.
Читать дальше

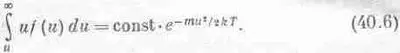
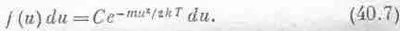
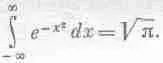
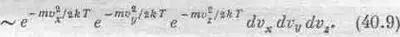



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)

