*) Первое точное измерение скорости звука в воздухе было сделано в коллективной работе членов Парижской академии наук в 1738 г. Измерялось время, за которое звук пушечного выстрела проходит 30 км. Чтобы исключить влияние ветра, выстрелы производились одновременно из двух пушек, удаленных друг от друга на 30 км.
Правильное объяснение этому расхождению нашел Лаплас, заметивший, что при прохождении звуковой волны температура воздуха в местах сгущения и разрежения различна, и законом Бойля—Мариотта пользоваться нельзя. Вместо этого Лаплас предположил, что изменения состояния газа в звуковой волне происходят столь быстро, что тепло не успевает передаваться от нагревшихся сжатых участков к охладившимся разреженным, т. е. процесс происходит адиабатически **). Правильность его объяснения оспаривалась еще лет тридцать. Тем не менее общая теория волновых процессов уже в начале века твердо стояла на ногах и быстро завоевывала новые области для своих приложений.
**) См. книгу: Смородинский Я. А. Температура. — 2-e изд.— М.: Наука, 1987. — Библиотечка «Квант», вып. 12.
Особенно важно это было для волновой теории света. В работах Френеля волновая теория была настолько основательно разработана, что успешно объясняла не только явления, известные до ее победы, но и подсказывала новые. Единственная неудача постигла волновую теорию в объяснении явлений дисперсии света . Как и в теории звука, в оптике Френеля скорость волны могла изменяться в разных средах, но зависимости скорости от длины волны в одной среде не получалось. Пуассон даже после описанных в ч. 1 опытов сомневался в правильности теории Френеля. Его главное возражение как раз было связано с проблемой дисперсии. В ответе Пуассону Френель указал на молекулярную структуру вещества как на возможный источник дисперсии. К сожалению, ранняя смерть не позволила Френелю развить эту идею, но ее подхватил Коши.
Дисперсия волн в цепочке атомов
Связь дисперсии с атомной структурой проще всего понять в нашей пружинной модели. Хотя при этом речь идет о звуковых, а не о световых волнах, суть дела одна и та же. Эту мысль и развил Коши. Найдем вслед за ним дисперсионную формулу для волн в цепочке «атомов», соединенных пружинками. Вспомнив то, что мы знаем о связи дискретной цепочки со сплошным стержнем, попробуем сразу написать решение всех уравнений (5.8) в виде бегущей волны ( 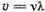 ):
):
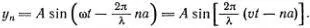
Если, как это делалось раньше, заменить nα на х и y n( t ) на y n( t , х ), то получится знакомая синусоидальная бегущая волна. Ее скорость v определяется из условия постоянства фазы (ω t - 2π х /λ). Поэтому скорость v называют фазовой скоростью . Если двигаться со скоростью v , то волна будет казаться неподвижной.
Так как 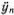 = -ω 2 y n, то из (5.8) следует простое уравнение
= -ω 2 y n, то из (5.8) следует простое уравнение
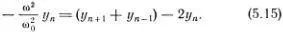
С помощью известной формулы для преобразования суммы синусов двух углов в произведение легко найти, что для синусоидальной волны y n+1 + y n-1= 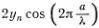 .
.
Подставляя это в уравнение (5.15), легко увидеть, что оно выполнено сразу для всех n , если
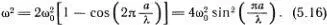
Это и есть дисперсионная формула Коши. Если длина волны много больше расстояния между атомами, т. е. 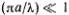 , то sin (π α /λ)
, то sin (π α /λ)  π α /λ и ω
π α /λ и ω  2πω 0( α /λ). При этом дисперсия исчезает, так как скорость не зависит от λ: v (λ) = ωλ/2π
2πω 0( α /λ). При этом дисперсия исчезает, так как скорость не зависит от λ: v (λ) = ωλ/2π  α ω 0=
α ω 0= 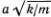 = v . Этот результат мы уже получили раньше при переходе к «непрерывному» пределу (см. формулу (5.14)). Если длина волны сравнима с расстоянием между атомами, то скорость зависит от λ:
= v . Этот результат мы уже получили раньше при переходе к «непрерывному» пределу (см. формулу (5.14)). Если длина волны сравнима с расстоянием между атомами, то скорость зависит от λ:
Читать дальше

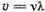 ):
):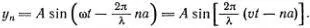
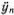 = -ω 2 y n, то из (5.8) следует простое уравнение
= -ω 2 y n, то из (5.8) следует простое уравнение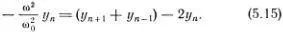
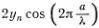 .
.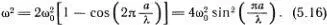
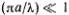 , то sin (π α /λ)
, то sin (π α /λ)  π α /λ и ω
π α /λ и ω 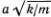 = v . Этот результат мы уже получили раньше при переходе к «непрерывному» пределу (см. формулу (5.14)). Если длина волны сравнима с расстоянием между атомами, то скорость зависит от λ:
= v . Этот результат мы уже получили раньше при переходе к «непрерывному» пределу (см. формулу (5.14)). Если длина волны сравнима с расстоянием между атомами, то скорость зависит от λ:










