Понимание связи между ньютоновской дискретной средой (от лат. discгetus — прерывистый, разделенный) и эйлеровой непрерывной средой очень важно, так как в разных случаях удобно переходить от дискретного языка к непрерывному и обратно.
Например, если изучаются упругие волны в кристаллах, то обычно можно забыть об их атомной структуре и считать кристалл просто непрерывной упругой средой. Атомная структура скажется на том, что упругие свойства кристалла будут разными в разных направлениях. Мы, однако, пойдем намеченным путем, так как у нас есть надежные уравнения (5.8), описывающие движения каждой точки дискретной системы.
Предположим для определенности, что грузопружинная модель, изображенная на рис. 5.1, должна приближенно воспроизводить продольные колебания и волны в упругом стержне. Точно так же можно рассмотреть звуковые волны в трубе, поперечные колебания струны и т. п. Идея перехода к непрерывной среде ясна: нужно уменьшать массы грузиков и длины пружинок так, чтобы средняя линейная плотность (т. е. масса на единицу длины ρ 1= m/α) и упругость пружины оставались постоянными.
Сначала надо немного точнее определить, что такое упругость пружины. В правой части уравнения (5.8) написана сила, действующая на n -й грузик при растяжении n -й пружины с длиной α на величину Δ l : F = k ( y n+1- y n) = k Δ l . Значение коэффициента k должно подбираться так, чтобы стержень и пружинная система одинаковой длины растягивались на одну и ту же величину под действием одной и той же силы.
Удлинения стержня и пружины пропорциональны их длине. Например, если пружинка удлиняется на Δ l , то обе ее половинки удлиняются на Δ l /2. Это значит, что коэффициент k для пружинки длиной α/ 2 равен просто 2 k . Поэтому, записав силу F = k Δ l в виде F = kα( Δ l/α) , мы получим характеристику упругости пружины, не зависящую от ее длины: для пружины любой длины α величина kα = К одна и та же. Для стержня любой длины l также будет верно соотношение F = К( Δ l/l ). Значение К определяется только упругостью стержня и не зависит от его длины.
Уравнение (5.8) легко переписать так, чтобы оно зависело лишь от ρ 1= m / α и К = kα , а не от m и k . После этого можно показать, что для волн, длина которых много больше α , можно при достаточно малых значениях α описать распространение волн в стержне уравнением Д'Аламбера

Движение каждой частицы стержня определяется, если известно решение у ( t, х ) этого уравнения: у n ( t ) = y (t, x = nα ). Скорость распространения упругих волн по стержню очевидно равна 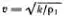 . В качестве упражнения попробуйте «вывести» уравнение (5.12) из уравнения (5.8).
. В качестве упражнения попробуйте «вывести» уравнение (5.12) из уравнения (5.8).
Скорость распространения волн по цепочке можно найти, и не прибегая к уравнению Д'Аламбера. Если по цепочке бежит волна неизменной формы со скоростью v , то она перемещается на расстояние α за время Δ t = α / v .
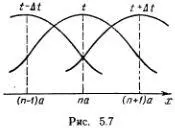
Отсюда следует, что y n-1( t ) = y n( t + Δ t ) и y n+1( t ) = y n( t - Δ t ) (рис. 5.7). Если рассматривать y n( t ) как график движения некоторой точки, то 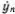 ( t ) будет скоростью, а
( t ) будет скоростью, а 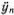 ( t ) — ускорением точки. Приближенно считая движение от момента t - Δ t до момента t + Δ t равномерно ускоренным, можно написать
( t ) — ускорением точки. Приближенно считая движение от момента t - Δ t до момента t + Δ t равномерно ускоренным, можно написать
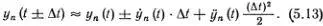
Подставляя полученные таким способом выражения для y n-1( t ) и y n+1( t ) в уравнение (5.8), находим, что [ m - k (Δ t ) 2] 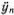 ( t ) = 0. Отсюда следует, что (Δ t ) 2= m/k (предполагается, конечно, что в какой-нибудь момент времени
( t ) = 0. Отсюда следует, что (Δ t ) 2= m/k (предполагается, конечно, что в какой-нибудь момент времени 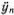
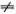 0). Для скорости волны v = α /Δ t находим поэтому выражение
0). Для скорости волны v = α /Δ t находим поэтому выражение
Читать дальше


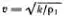 . В качестве упражнения попробуйте «вывести» уравнение (5.12) из уравнения (5.8).
. В качестве упражнения попробуйте «вывести» уравнение (5.12) из уравнения (5.8).
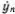 ( t ) будет скоростью, а
( t ) будет скоростью, а 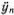 ( t ) — ускорением точки. Приближенно считая движение от момента t - Δ t до момента t + Δ t равномерно ускоренным, можно написать
( t ) — ускорением точки. Приближенно считая движение от момента t - Δ t до момента t + Δ t равномерно ускоренным, можно написать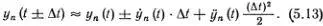
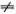 0). Для скорости волны v = α /Δ t находим поэтому выражение
0). Для скорости волны v = α /Δ t находим поэтому выражение










