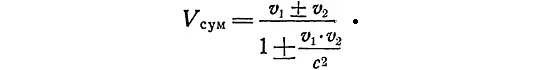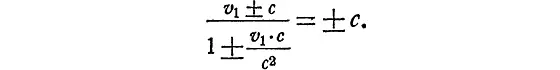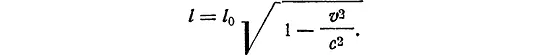Вольдемар Смилга - Очевидное? Нет, еще неизведанное…

В классической механике суммарная скорость определялась предельно простым выражением v сум = v 1 ± v 2(знак + в том случае, когда стреляют по ходу поезда, и знак –, когда против хода).

По Эйнштейну, закон для определения суммарной скорости другой:

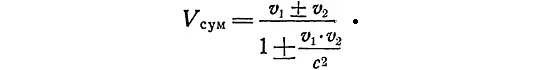
Как видно, если v 1 << c и v 2 << c , формула Эйнштейна переходит в классическую. (В этом случае можно спокойно пренебречь вторым членом знаменателя по сравнению с единицей.) Если же скорости v 1и v 2сравнимы со скоростью света, тогда формула Эйнштейна становится совершенно отличной от классической.

Лучше всего в этом можно убедиться, положив одну из скоростей (например, v 2) равной скорости света. Если помните, мы уже упоминали об этой задаче, обсуждая в XI главе, какова будет относительно полотна дороги скорость светового луча, посланного источником, находящимся на поезде. Легко видеть, что независимо от v 1абсолютная величина суммарной скорости снова равна скорости света.

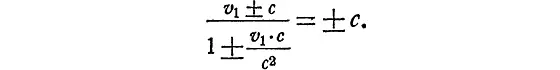
Теперь можно разбить наши рассуждения в XI главе. Как помните, там, защищая баллистическую гипотезу, мы принимали как самоочевидный факт классическую формулу сложения скоростей.

И вот, как оказывается, именно это и неправильно.

Фронт световой волны, идущей из прожектора поезда, распространяется со скоростью с относительно поезда. Но относительно наблюдателя на земле он распространяется не со скоростью ( v поезда + c ), а снова с той же скоростью c .

Для нашего воображения, воспитанного на классической механике, это удивительно. Удивительно, но тем не менее правильно.

Более того, относительная скорость двух фотонов, несущихся навстречу друг другу со скоростью света, снова равна c , а не 2 c , как в классической физике [70] .

В механике Эйнштейна скорость света в вакууме представляет барьер, через который невозможно перебраться.

Как измерять длину движущихся тел, мы уже договорились в III главе. Напомним: «Длина движущегося тела есть расстояние между одновременно отмеченными положениями его начальной и конечной точек».

В классической физике длина движущегося тела, определенная таким образом, совпадала с длиной неподвижного тела, и все было хорошо. Еще и еще раз напомним:

1. До Эйнштейна вообще никто не задумывался, «как определяется длина движущихся тел». Но, по сути дела, каждый раз, измеряя длину или говоря о ней, молчаливо подразумевали, что она определяется именно так, как сказано выше.

2. Совпадение или несовпадение длин покоящегося и движущегося тела — это вопрос опыта, и никак нельзя утверждать заранее, что они должны совпадать.

Не следует навязывать природе наши взгляды и желания. В данной конкретной системе отсчета, где проводятся изменения, стержень неподвижный и стержень движущийся находятся в разных физических условиях, и нет никаких оснований ожидать, что длина не изменяется при движении. Так думали раньше, бессознательно обобщая эксперименты. Ведь в обычных опытах исключительно трудно наблюдать различие в длинах движущегося и неподвижного предмета, ибо достижимые скорости материальных тел неизмеримо меньше скорости света. Поэтому и не наблюдалось никакого изменения длины, а отсюда уверенность, что длина предмета абсолютна и неизменна независимо от того, из какой системы отсчета ее определяют.

Но… самый непосредственный анализ преобразований Лоренца показывает, что длина — величина относительная.

Действительно, длина стержня, движущегося со скоростью v, сокращается в направлении движения и определяется выражением:

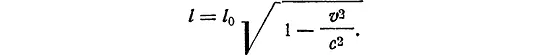
где l 0— длина стержня, когда он находится в состоянии покоя [71] , то есть длина, измеренная в той системе отсчета, в которой стержень покоится. Этот эффект и называется лоренцовым сокращением длины [72] .