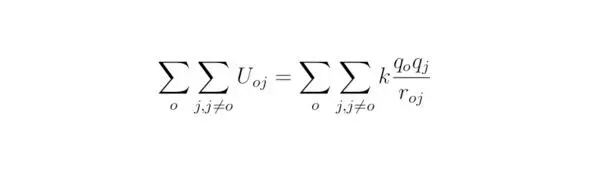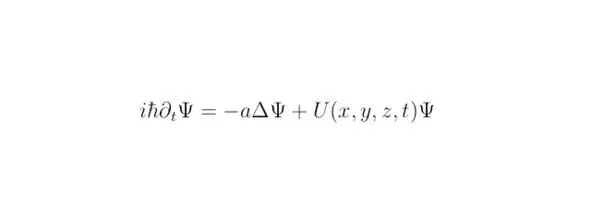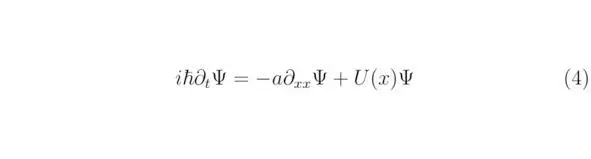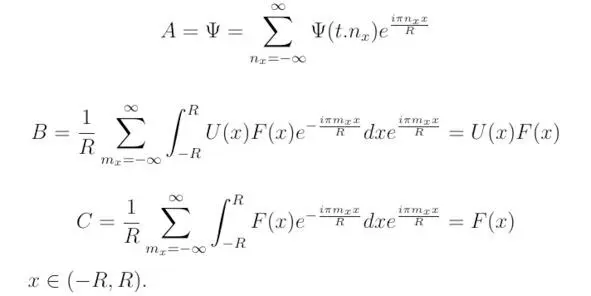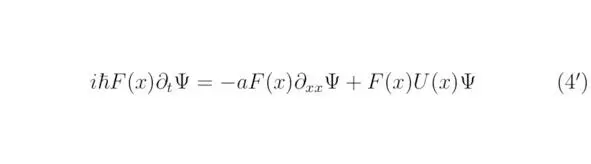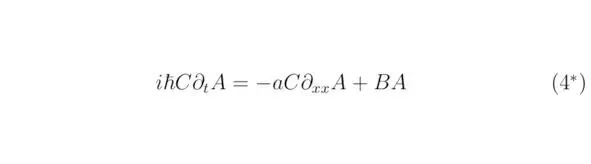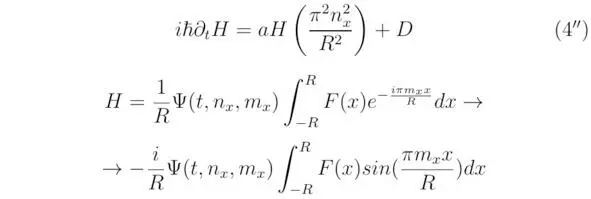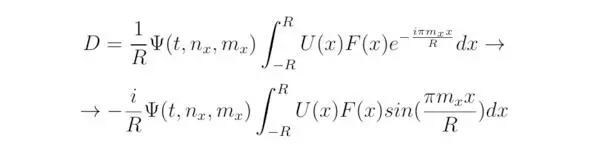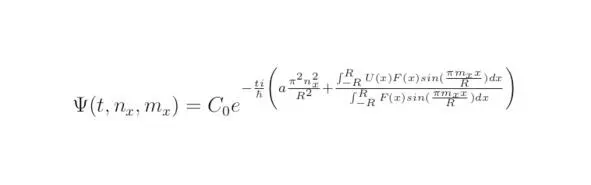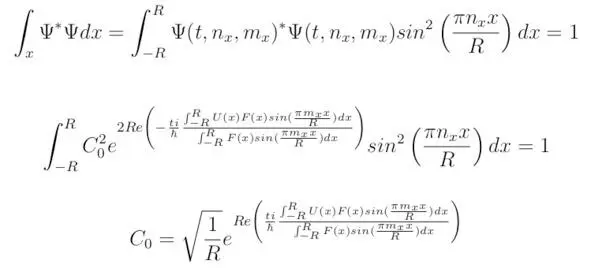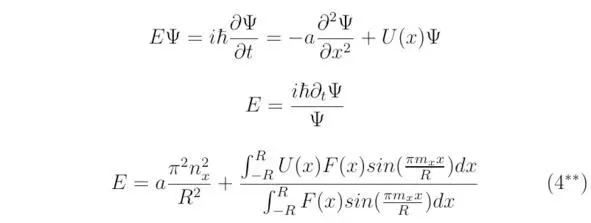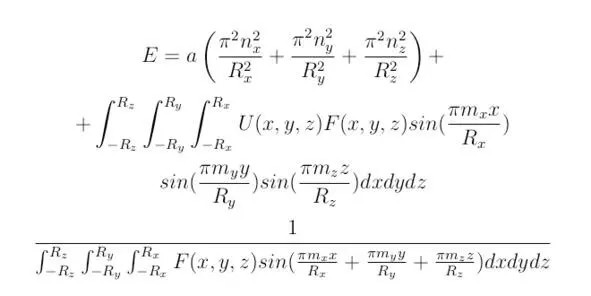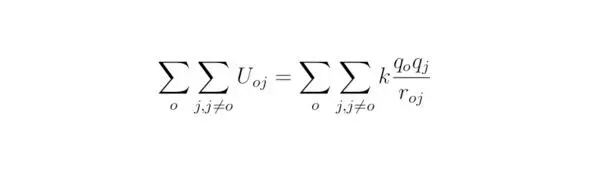
где r oj – расстояние между частицами под номерами o и j, q j, q o – заряды частиц, k – коэффициент пропорциональности.
Волновая функция ψ – комплекснозначная величина, используемая в квантовой механике для описания чистого состояния системы, когда квантово-механические процессы протекают без декогеренции. Волновая функция физического смысла не имеет, но физический смысл приписывается плотности вероятности.
В следующем параграфе мы получим общее аналитическое решение уравнения Шрёдингера. Применяя последнее на практике, можно обобщить большинство явлений нерелятивистской квантовой механики, в том числе дать математическое обоснование редукции Фон Неймана (коллапсу волновой функции).
4. К аналитическому решению уравнения Шрёдингера в С n
В данной главе будет проанализирован новый подход к решению дифференциальных уравнений. В качестве примера мы рассмотрим решение уравнения Шрёдингера, полученное в декартовой системе координат для одной частицы. Согласно положениям раздела 2, исследуемое уравнение можно записать в следующей форме:
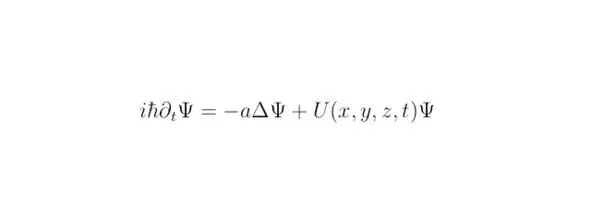
здесь a=ħ 2/ (2M). Волновая функция ψ выражена семейством функций. Символом Δ обозначают сумму операторов ∂ 2/∂x 2+∂ 2/∂y 2+∂ 2/∂z 2…, знак ∂ tэквивалентен частной производной ∂/∂t. Уравнение Шрёдингера, полученное для одномерного случая, возможно преобразовать к виду:
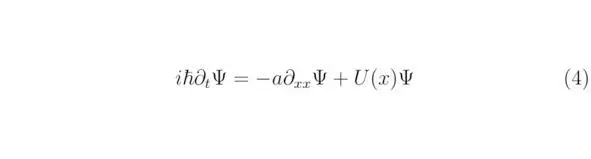
4.1 Пример решения уравнения Шрёдингера
Осуществляя поиск аналитического решения уравнения Шрёдингера, необходимо разложить в ряд Фурье величину ψ, а также выражения F (x) и U (x) F (x), следовательно:
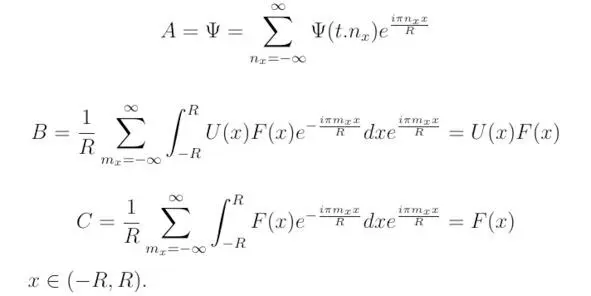
здесь F (x) – произвольно заданная дифференцируемая функция, F (x) ∈ C; -R, R – координаты граничных условий.
Выполним следующие преобразования:
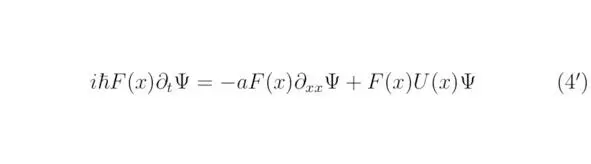
Заменим неизвестные переменные в тождестве (4`) на соотношения A, B, C, тогда:
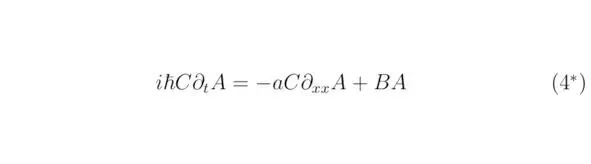
Выражение (4 *) содержит в себе общий член exp (iπm xx/R) exp (iπn xx/R). Необходимо сократить последний, оставив в результате только коэффициенты тригонометрического ряда:
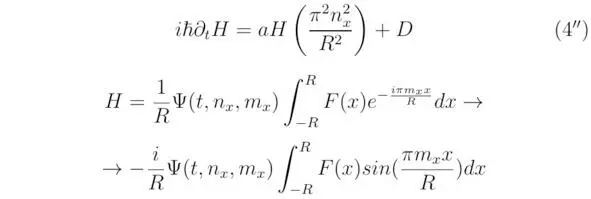
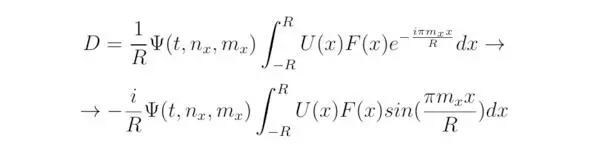
Разделим переменные относительно ψ (t, n x, m x), тогда:
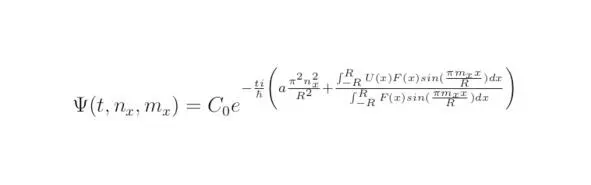
Коэффициент C 0возможно определить исходя из соотношения, полученного для нормированной вероятности (см. раздел 3.3). В рассматриваемом примере существует зависимость величины C 0от времени t. Таким образом, следует потребовать постоянство коэффициента C 0в случае решения стационарного уравнения Шрёдингера.
Область определения волновой функции будет лежать в пределах отрезка (-R,R). В некоторых теоретических случаях допустимо принимать R=∞, тогда:
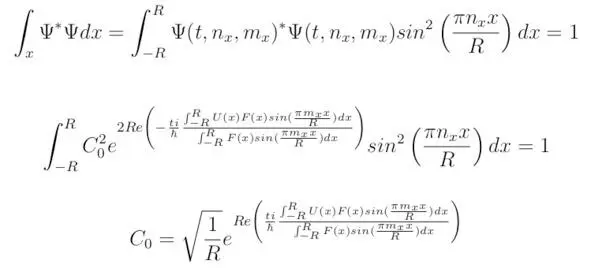
Энергию электрона E можно определить из стационарного одномерного уравнения Шрёдингера, следовательно:
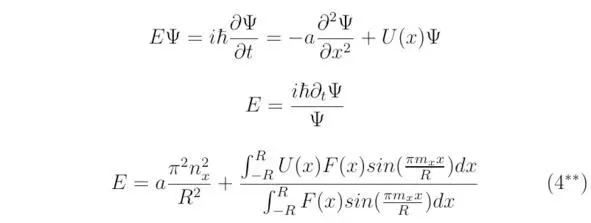
Для трёхмерного базиса величина полной энергии составит:
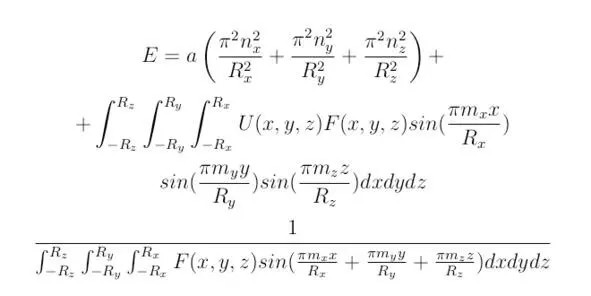
В заключение следует отметить, что величина E часто не обладает конкретно заданным значением, поскольку в выражении, полученном для полной энергии E, присутствуют произвольные функции: F (x) для одномерной или F (x,y,z) для трёхмерной системы координат. Исходя из неопределённости величины E, находящейся в зависимости от значений непостоянной потенциальной энергии U (x,y,z) ≠const, вид функций F (x) и F (x,y,z) установить невозможно.
Читать дальше