Игорь Мерзляков - Путешествие в квантовую механику

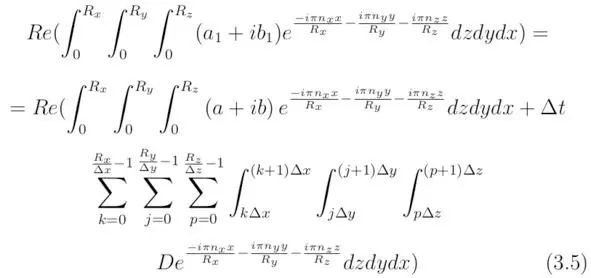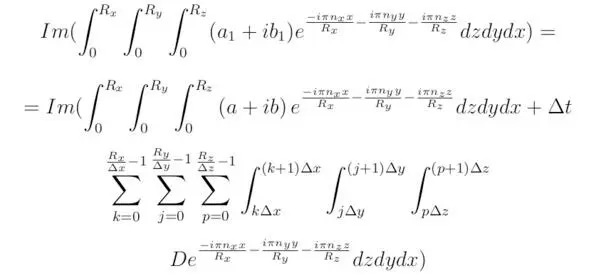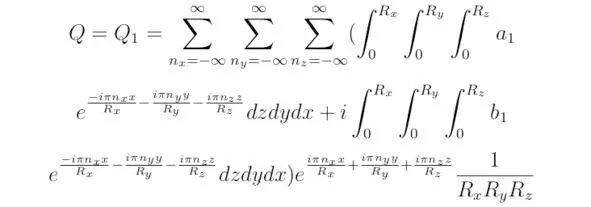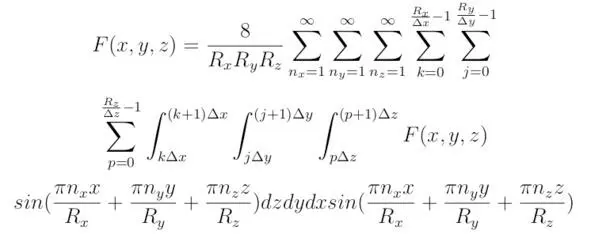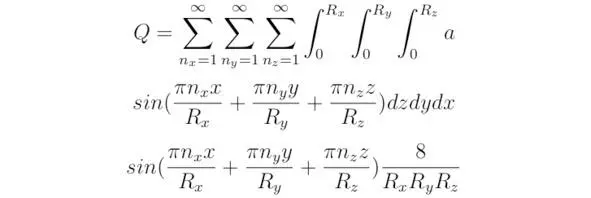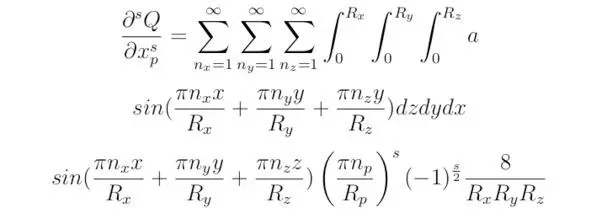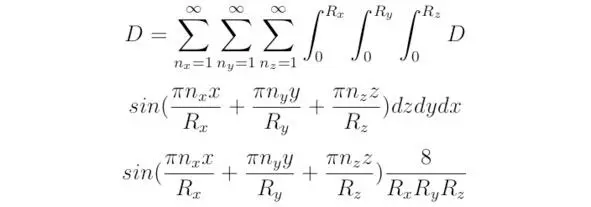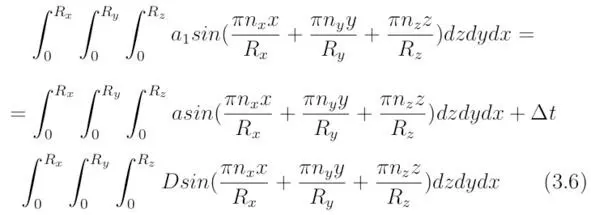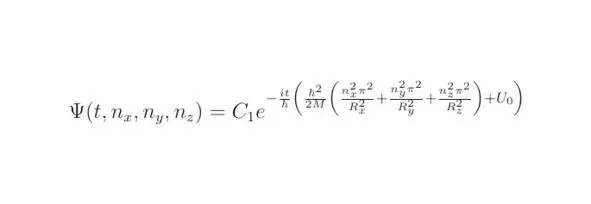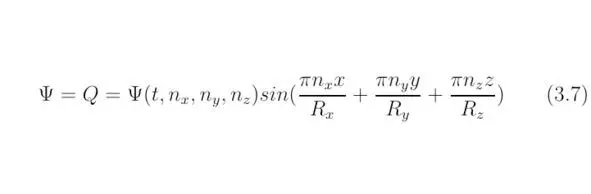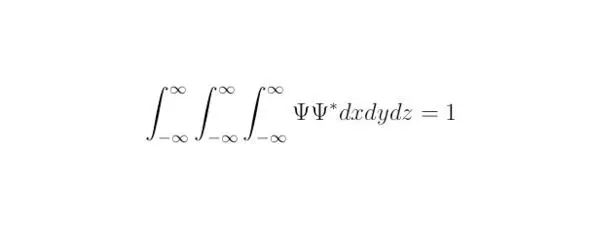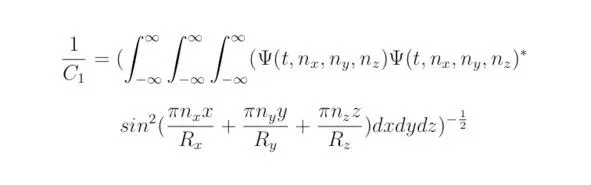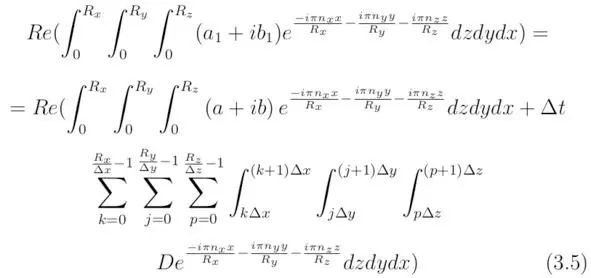
Вместе с тем справедливым будет тождество, полученное для мнимой части уравнения (3`):

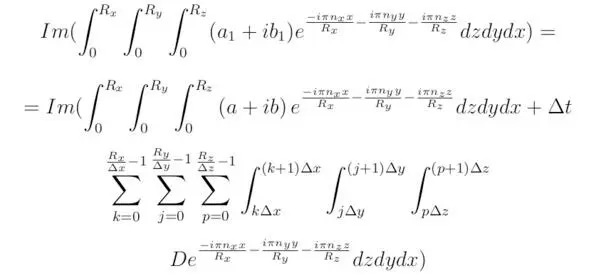
где Re (Q) и Im (Q) – вещественная и мнимая части функции Q.

С каждой новой итерацией по времени вместо выражения Q следует подставлять известное решение Q 1, тогда:

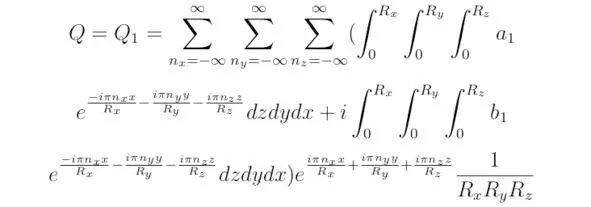
В процессе расчёта переход к уравнению (3.1) необходимо выполнять до тех пор, пока не будет достигнуто условие VΔt=T, здесь T – промежуток времени, определяющий эволюцию искомой функции Q, Δt – величина шага по времени, V – общее количество итераций.

В предыдущем подразделе мы рассмотрели методику, с помощью которой можно отыскать решение того или иного дифференциального уравнения. Разбирая частный случай данной задачи, необходимо потребовать, чтобы исследуемое дифференциальное уравнение было линейным. Если величины n x, n y, n z окажутся положительными, то справедливым будет следующее условие Q∈ R. Таким образом, тождество (3 *) возможно свести к виду:

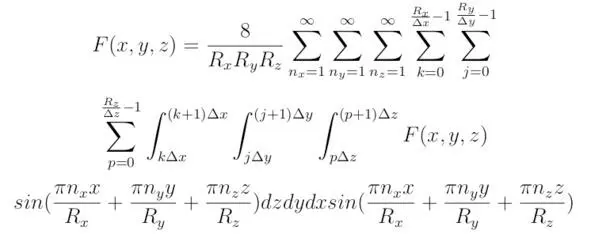
Преобразуем выражение (3.1), тогда:

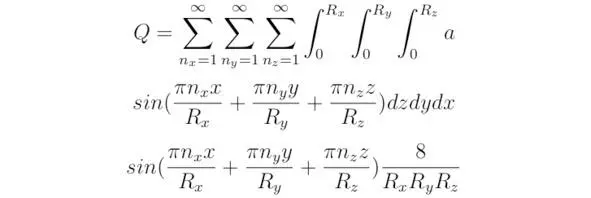
Соотношение (3.3), полученное для операции дифференцирования, можно свести к виду:

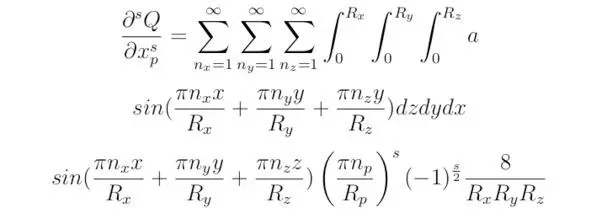
для всех чётных s. где p – индекс координаты.

Преобразовав выражение D, справедливым будет записать следующее тождество:

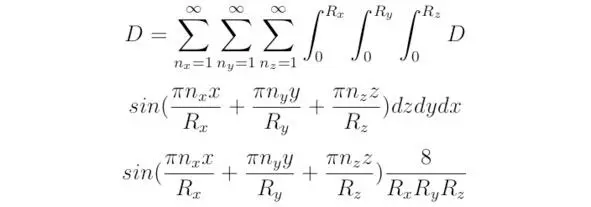
Уравнение (3`) можно представить в виде соотношения:

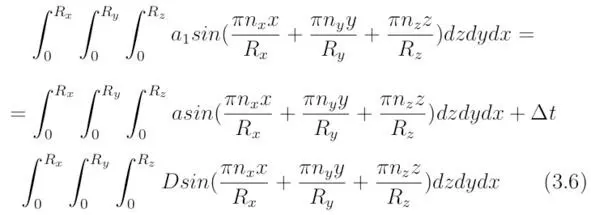
Коэффициенты Фурье, которые соответствуют следующей по времени итерации, легко можно выразить через коэффициенты Фурье, полученные для предыдущей итерации.

Уравнение Шрёдингера, составленное для постоянной потенциальной энергии, является линейным. Вместе с тем коэффициенты s, входящие в состав рассматриваемого дифференциального уравнения, будут чётными. Таким образом, существует возможность разрешить уравнение Шрёдингера, применяя методику, изложенную выше. Более того, если подставить в качестве решения функцию Q=ψ (t) ψ (x) ψ (y) ψ (z), тогда справедливым будет следующее выражение:

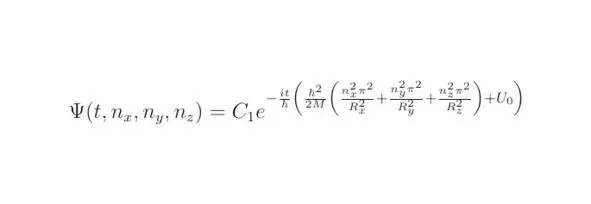
Частное решение уравнения Шрёдингера возможно представить в виде соотношения:

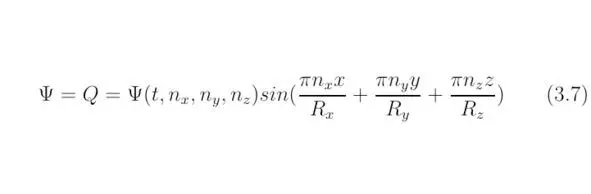
Общее решение является суммой частных по п x, n y, n z.

Под обозначением ψ * понимается комплексно сопряжённая волновая функция. Плотностью вероятности появления частицы в точке с координатами (x,y,z) называют соотношение ψψ *. Коэффициент C 1 можно определить исходя из тождества ограниченности вероятности:

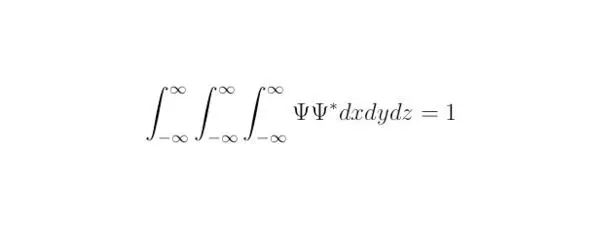
Следовательно:

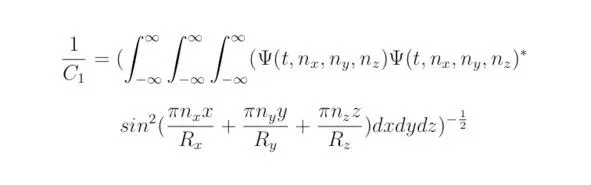
где n x, n y, n z – коэффициенты, определяющие дискретные значения полной энергии квантовой системы.

На практике нередко можно встретить ситуацию, когда вместо потенциальной энергии в уравнение Шрёдингера подставляется постоянный коэффициент (потенциал). Исходя из закона Кулона, составленного для энергий, возможно, например, определить условия существования неподвижных в пространстве молекулярных и кристаллических структур. Атомы химического соединения будут сохранять свою стабильность до тех пор, пока сумма энергий Σ oΣ j, j≠oU oj, полученная для всех кулоновских взаимодействий, не изменит своего значения. Тогда: