Игорь Мерзляков - Путешествие в квантовую механику

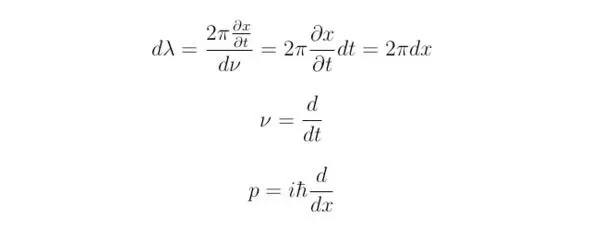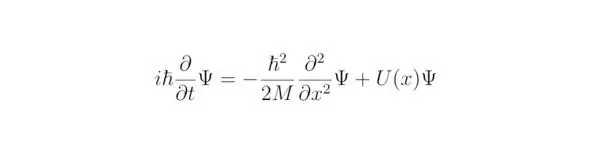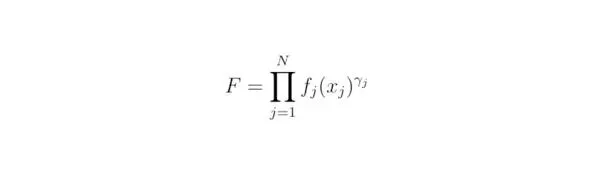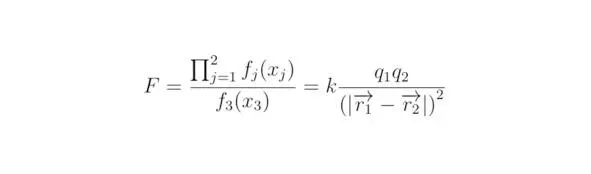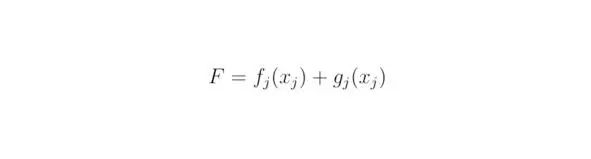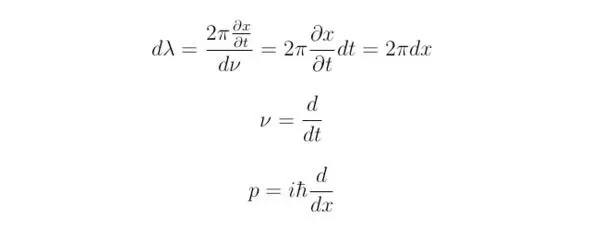
где t – время, а x – координата.

Следствие, которое можно почерпнуть из данных преобразований, гласит, что для справедливости выкладок, полученных в результате вывода уравнения Шрёдингера, необходимо ввести новую функцию под знаки производных. В процессе преобразований был найден оператор, который представляет из себя закон сохранения энергии, записанный для исследуемой волны Де Бройля. Искомую величину принято обозначать как волновую функцию ψ, тогда:

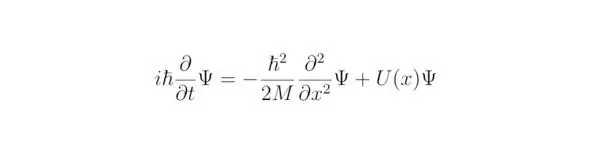
Последнее выражение носит своё название в честь учёного, который обобщил в своих научных исследованиях физические законы, описывающие волновую природу реальности. Главным достижением Эрвина Шрёдингера стало уравнение, сыгравшее огромную роль в развитии теоретических и практических результатов в квантовой физике. Общий вид уравнения Шрёдингера мы получили в этом параграфе.

Обычно с изучением школьной программы принято брать на веру справедливость основных положений, позволяющих осуществить вывод фундаментальных законов физики. В этом разделе мы разберём принципы получения таких зависимостей, которые существуют между физическими величинами, входящими в состав указанных законов.

Для того, чтобы выполнить дальнейшие математические преобразования, необходимо определить понятие «зависимости физических величин», значения которых могут быть выражены через изменение прочих независимых переменных.

Исходя из формулировки о зависимости величины F от функций f j(x j), полученных для переменных x j, заданные выражения f j(x j) следует перемножать между собой только в том случае, когда они окажутся независимыми. Иначе говоря, изменение функции f j(x j) будет происходить без взаимного влияния её значений на другие выражения f o(x o), o≠j. Потребуем, чтобы количество независимых переменных соответствовало величине N. Итак, функцию F можно выразить в виде соотношения, куда входят значения γ j. Каждое из значений γ jсоответствует коэффициенту пропорциональности (+1 или -1), который представляет из себя степень функции f j(x j) γj, следовательно:

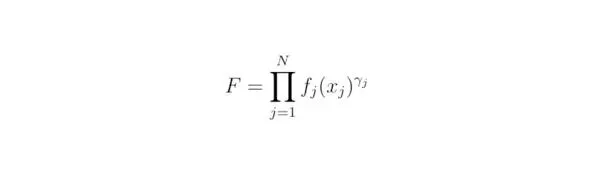
Наглядным примером применения эмпирического подхода к решению физических задач может послужить закон Кулона, полученный для силы электростатического взаимодействия. Таким образом, следующие выражения могут быть определены как независимые между собой функции:

f 1(x 1) – произведение зарядов q 1q 2.

f 2 – коэффициент пропорциональности k.

f 3(x 3) – квадрат расстояния между частицами f 3(x 3) =|r 1-r 2| 2. r p – радиус-вектор, построенный из начала координат в точку с зарядом q p. p=1,2.

Хорошо известно, что сила Кулона прямо пропорциональна f 1(x 1) и f 2(γ j=1), но обратно пропорциональна f 3(x 3) (γ 3=-1).

Запишем закон Кулона, вид которого можно получить из анализа экспериментальных данных:

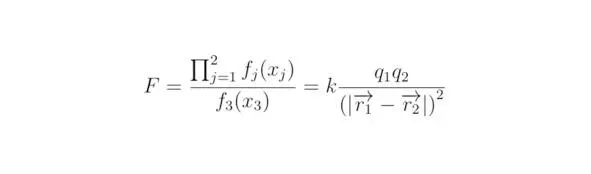
Если величины f j(x j) и g j(x j) окажутся взаимно зависимыми, тогда справедливым будет тождество:

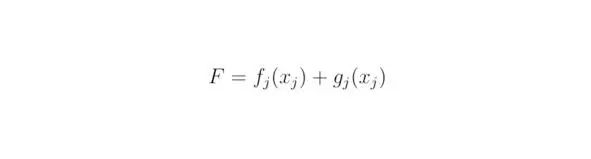
Функции f j(x j) и g j(x j) могут носить более сложный математический характер, нежели степенные выражения. Довольно часто эмпирическим методом невозможно получить тот или иной закон природы, тогда исследователи прибегают к составлению дифференциальных уравнений, например, дифференциальных уравнений в частных производных. Решение последних иногда затрудняется, вследствие невысокой производительности современных компьютеров, в подобных случаях используют суперкомпьютеры.

Пришло время ознакомиться с третьим разделом этой книги, где мы сформулируем общее представление о трудностях, возникающих в процессе решения уравнения Шрёдингера. В следующей главе будет рассмотрен метод, позволяющий отыскать решение произвольно заданного дифференциального уравнения в частных производных.