Александр Астахов - Физика. Порядок вещей, или Осознание знаний. Книга 2

Таким образом, трёхточечная схема может давать не достоверную информацию, какое ускорение есть на каждом из смежных участков и какие расстояния пройдены с ускорением и без него.

Рассмотрим этот вопрос более подробно на примере поворотного движения Кориолиса, ускорение которого в соответствии с приведённым физическим механизмом явления Кориолиса вдвое меньше классического.

На рисунке (4.1.1.3) приведена классическая трёхточечная схема применительно к криволинейному движению. Временной интервал между точками (1, 2, 3), как и прежде – одна секунда. Очевидно, что если бы не было радиальной скорости, то все три радиуса-вектора (DK), (D «2»), и (DL) были бы одинаковыми. При этом разница проекций (DK) и (DL) на ось (Y) была бы равна нулю (ВD – DF = 0), что означает отсутствие ускорения вдоль тангенциального направления (Y).

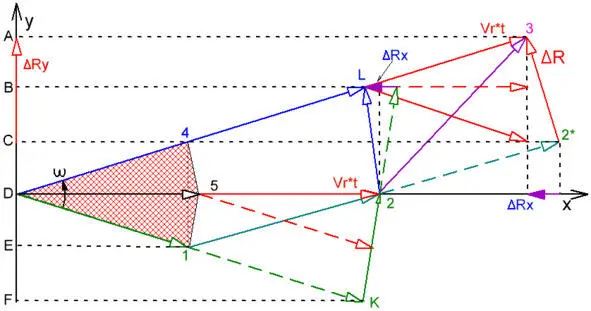
Рис. 4.1.1.3

Очевидно, что с учётом радиального движения радиус-вектор (D «1») будет короче радиуса-вектора (DK) на («1» К = Vr * t * sin (ω * t)), а радиус-вектор (D «3») длиннее радиуса-вектора (DL) на величину (L «3» = Vr * t * sin (ω * t)). А поскольку разность проекций на ось (Y) областей (D «4» «5») и (D «5» «1») равна нулю (красная штриховка), то приращение вдоль оси (Y) соответствует двум проекциям приращения радиуса – (AC = АВ + ВС = 2 * Vr * t * sin (ω * t)). Это следует также и из операций с векторами – («2» «3» – «2» «2*» = «2*» «3» = AC = AD – DЕ = 2 * Vr * t * sin (ω * t)) или для малых углов (AC = 2 * Vr * ω * t 2). Однако это справедливо только в отсутствие истинной силы Кориолиса-Кеплера.

Как показано выше, в классическом поворотном движении половина поддерживающей вращение силы компенсирует истинную силу Кориолиса-Кеплера. При этом, несмотря на изменение радиуса, исходная линейная скорость в общем составе переменного движения сохраняется неизменной. Эта постоянная скорость не причастна к ускорению Кориолиса, т.к. она возникает в результате равновесия сил. Следовательно за ускорение Кориолиса ответственна только оставшаяся неуравновешенная половина поддерживающей силы. Однако трёхточечная схема «не видит» непричастную к неуравновешенному движению половину.

Действительно, из рисунка (4.1.1.3) видно, что приращение поворотного движения вдоль оси (Y), равное (AC = 2 * Vr * ω * t 2)) при вычитании смежных участков остаётся не скомпенсированным ни в какой своей части, как например, это происходит с проекциями областей (D «4» «5») и (D «5» «1»). Следовательно не скомпенсированной в составе этого общего приращения остаётся и приращение, обусловленное постоянной линейной скоростью, которая как мы отмечали выше не причастно к ускорению Кориолиса. В результате классическое ускорение Кориолиса вдвое больше реального.

Таким образом, полное напряжение Кориолиса в статике действительно соответствует классической силе Кориолиса (Fпк = 2 * m * Vr * ω). Однако динамические ускорение и сила Кориолиса оказываются при этом вдвое меньше классических аналогов ( а кд= Vr * sin (ω * t) / t = Vr * ω, Fкд = m * Vr * ω).

Математически коррекция трёхточечной схемы может быть выражена, как через произведение (Vr) на синус половины угла поворота (ω * t / 2), так и через прежний угол, но с коэффициентом «1/2» перед всем произведением, а также через средний радиус поворота – (Rср. = Vr * t / 2). Графически откорректировать классическую трёхточечную схему по среднему радиусу, можно сократив (L «3») и («1» S) ровно на половину (см. Рис. 4.1.1.3). При этом из каждого участка уйдёт и их постоянная часть (условно – это (AM) и (NF)), образующаяся за счёт компенсации истинной силы Кориолиса-Кеплера (см. Рис. 4.1.1.4).

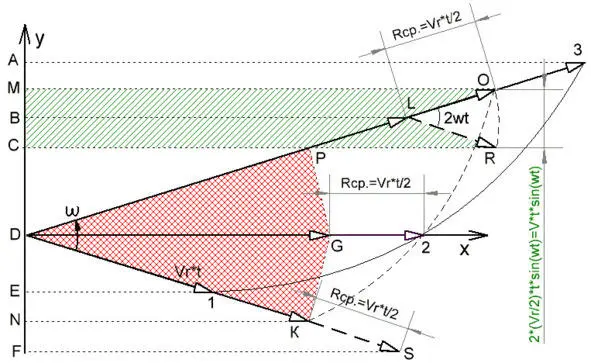
Рис. 4.1.1.4

Как видно, при вычитании смежных участков проекции области (DPG) и (DGK) на ось (Y) взаимно уничтожаются (красная решётчатая штриховка). При этом реальное приращение пути будет вдвое меньшим, чем до коррекции (МD – DE = МС = МВ + ВС = 2 * (Vr / 2) * t * sin (ω * t) = Vr * t * sin (ω * t)) (зелёная косая штриховка). Естественно, что при этом изменятся также и координаты откорректированной схемы. Вместо координат точек («1» «2» «3), равных соответственно (ЕDА) будут координаты точек (K «2» O), равные соответственно (MDN).

Однако в этом нет никакого противоречия, т.к. это уже не траектория реального движения, а эквивалентная схема для вычисления истинного приращения пути. При этом определять новые координаты естественно нет никакой необходимости. Достаточно, математической коррекции полученного по трёхточечной схеме результата. Вывод ускорения Кориолиса через средний радиус будет приведён ниже (см. вывод Кухлинга, гл. 4.1.1.2.).