Александр Астахов - Физика. Порядок вещей, или Осознание знаний. Книга 2

Площадь, описываемая радиус-вектором за малое время Δt, приближенно равна площади треугольника с основанием rΔθ и высотой r:

dS = ½ * r 2* Δθ

dS / dt = ½ r 2* dθ / dt = ½ * r * V ┴= ½ * ω * r 2= const.

А поскольку секторальная скорость (dS / dt) постоянна, то её производная по времени S’t равна нулю:

S«(t) = ½ (r’(t) * V ┴+ r * V ┴»(t)) = 0

где

r’(t) = Vr – радиальная скорость

V ┴»(t) = a К ист – ускорение Кориолиса Истинное;

V ┴= ω * r

Тогда:

Vr * ω * r + r * a К ист.= 0

Сократив на r, получим:

a К ист= – Vr * ω

Тогда Истинная сила Кориолиса равна:

Fк ист = а К ист* m = – Vr * ω * m

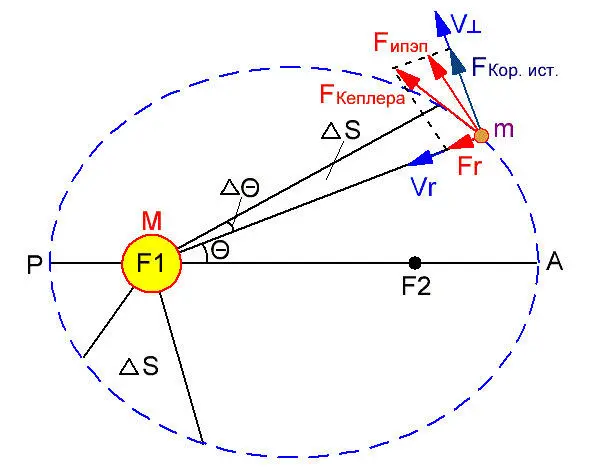
Не трудно показать связь второго закона Кеплера с так называемым законом сохранения момента импульса или углового момента классической лже динамики вращательного движения.

L = m * ω * r 2

Тогда:

dS / dt = ½ * L / m

Таким образом, угловая скорость при радиальном движении определяется не только чисто геометрическим масштабированием при неизменной линейной скорости с масштабным коэффициентом-радиусом, что совершенно очевидно и без каких-либо выводов, но и за счёт истинной силы Кориолиса-Кеплера, которая физически изменяет линейную скорость на каждом текущем радиусе. При этом истинная сила Кориолиса-Кеплера, тормозящая тело при радиальном движении от центра вращения и разгоняющая его при движении к центру, вдвое меньше классической силы Кориолиса. Напомним коротко физический механизм, лежащий в основе второго закона Кеплера, изложенный в главе (3.4.3), на примере радиального движения от центра вращения.

В результате ослабления связей с центром вращения при радиальном движении часть энергии связи безвозвратно рассевается в окружающем пространстве. При этом энергия связи, необходимая для установления нового вращения тела на новом радиусе, может быть изъята только из кинетической энергии освобождающегося тела. Отбор необходимой энергии осуществляется за счёт истинной силы Кориолиса-Кеплера, которая является тангенциальной проекции радиальной силы на касательную к спирали. При этом угловая скорость тела уменьшается, как геометрически в результате масштабирования между угловой и линейной скоростью с масштабным коэффициентом-радиусом, так и за счёт непосредственного физического уменьшения линейной скорости через силу Кеплера (см. гл. 3.4.3.).

Таким образом, классическая сила и ускорение Кориолиса, которые определяются при неизменной угловой скорости – есть результат компенсации воздействия на вращательное движение физических факторов характеризующих второй закон Кеплера. Это геометрическое масштабирование между угловой и линейной скоростью и истинная сила Кориолиса-Кеплера, которые и определяют физический смысл не только второго закона Кеплера, но и явления Кориолиса, а также произвольного криволинейного движения в целом, которого вне второго закона Кеплера, т.е. без истинной силы Кориолиса-Кеплера не бывает.

Очевидно, что в классическом поворотном движении при неизменной угловой скорости часть поддерживающей вращение силы компенсирует истинную силу Кориолиса-Кеплера. При этом исходная линейная скорость на новом радиусе остаётся неизменной. Эта равновесная часть поддерживающей силы не причастна к ускорению Кориолиса. Дальнейшее восстановление угловой скорости до исходного значения с ускорением Кориолиса осуществляется только за счёт оставшейся части поддерживающей силы. Напомним, что за силу Кориолиса в классической физике принимается реакция на поддерживающую силу.

Осталось выяснить количественное соотношение равновесной статической и неуравновешенной динамической части поддерживающей силы.

Из классической версии явления Кориолиса известно, что полная поддерживающая сила равна (Fпк = 2 * m * ω * Vr). Это вдвое больше истинной силы Кориолиса-Кеплера, равной (Fик = m * ω * Vr). Следовательно, оставшаяся после компенсации истинной силы Кориолиса-Кеплера динамическая часть поддерживающей силы и сообщаемое ей реальное тангенциальное ускорение Кориолиса, равны ровно половине поддерживающей силы. Соответственно реакция на эту динамическую часть поддерживающей силы, т.е. реальная сила Кориолиса, также вдвое меньше классической силы Кориолиса.

Это непосредственно следует из физического смысла второго закона Кеплера и чисто аналитически. Поскольку в отсутствие поддерживающей силы угловая скорость обратно пропорциональна квадрату радиуса, а геометрическое масштабирование угловой и линейной скорости через масштабный коэффициент-радиус обратно пропорционально только первой степени радиуса, то на долю статической и динамической части поддерживающей силы приходится ровно по половине её величины.