Александр Астахов - Физика. Порядок вещей, или Осознание знаний. Книга 2

А. Н. Матвеев в работе «Механика и теория относительности», 3-е издание, Москва, «ОНИКС 21 век», «Мир и образование», 2003 г., допущенной в качестве учебника для студентов высших учебных заведений определяет ускорение Кориолиса следующим образом (см. фотокопии ниже).

Книга написана в соответствии с программой курса физики для университетов, однако, физики в данном учебнике нисколько не больше, чем во многих других современных учебниках по физике. Форма написания книги больше соответствует справочной литературе по физике, в которой приводятся не столько физические, сколько математические описания физических явлений.

Матвеев пытается выяснить и донести до читателей « физическую сущность кориолисова ускорения» , как он сам пишет на странице 403 своей книги. Однако все принципиальные выводы, касающиеся физики явления Кориолиса, подробно не анализируются. Все спорные и противоречивые моменты явления Кориолиса остаются без доказательства и разъяснений. Механизм образования ускорения Кориолиса не раскрыт. Всё представлено на уровне голой математики, за которой не всегда виден физический смысл явлений, хотя в физике все должно быть наоборот.

Ускорение Кориолиса в первом варианте по Матвееву это изменение скорости тела, движущегося радиально внутри вращающейся системы в направлении, перпендикулярном радиусу вращения.Это общепринятое в классической физике определение ускорения Кориолиса.

На стр. 404 Матвеев пишет:

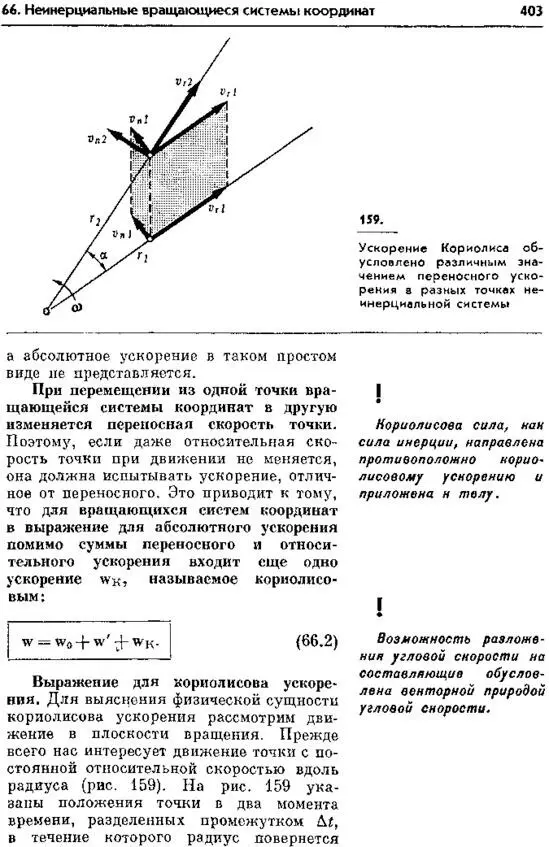
«Скорость вдоль радиуса Vr изменяется за это время (Δt) по направлению, а скорость Vn, перпендикулярная радиусу, изменяется как по направлению, так и по абсолютному значению . Полное изменение составляющей скорости, перпендикулярной радиусу, равно:

ΔVn = Vn 1 – Vn 2* cos α + Vr * Δα ≈

≈ ω * r 1 – ω * r 2+ Vr * ω Δt = V * Δr + Vr * ω Δt (66.3)

где учтено, что cos α ≈ 1

Следовательно, кориолисово ускорение в пределе при Δt→0 равно:

w к= ω * Δr / dt + Vr * ω = 2 * Vr * ω (66.4) ».

Вообще говоря, поворот вектора переносной скорости происходит под действием переносного центростремительного ускорения, которое проявляется в радиальном направлении и потому не имеет никакого отношения к поворотному ускорению Кориолиса. Поэтому векторы (V n1) и (V n2) можно сравнивать по абсолютной величине непосредственно без проецирования (V n2) на тангенциальное направление с учётом ( cos α ). Всё намного серьёзнее, чем ненужное в данном случае проецирование и связано с неправильными физическими представлениями классической физики о явлении Кориолиса.

Из выражения (66.4) следует, что ускорение Кориолиса – это изменение абсолютной скорости в направлении перпендикулярном радиусу, которое обеспечивается двумя самостоятельными независимыми ускорениями:

1. Ускорением, характеризующим приращение линейной скорости переносного вращения по абсолютной величине;

2. Ускорением, характеризующим приращение радиальной скорости относительного движения по направлению.

Этим собственно и объясняется «двойка» в ускорении Кориолиса. Но если предположить, что эти две якобы самостоятельные интерпретации ускорения Кориолиса представляют собой одну и ту же физическую величину, то под сомнение подпадает именно её удвоение.

В соответствии со вторым законом Кеплера, ошибочно называемом в классической лже динамике вращательного движения законом сохранения не существующей в природе физической величины – момента импульса, линейная и угловая скорость при изменении радиуса изменяется обратно пропорционально первой и второй степени радиуса соответственно. Но как известно единственной причиной изменения скорости (импульса) неизменной массы является только сторонняя сила. Найдём эту силу.

Из формулировки второго закона Кеплера (1609 г.) следует – радиус-вектор обращающегося тела заметает равные площади за равные промежутки времени (см. рисунок ниже). Здесь Fипэп – сила инерции поэлементной поддержки (сила инерции Ньютона). Сила Кеплера является результирующей Fr и Fипэп. А истинная сила Кориолиса – проекция силы Кеплера на перпендикуляр к «r».