Александр Астахов - Физика. Порядок вещей, или Осознание знаний. Книга 2

Если путём компенсации истинной силы Кориолиса-Кеплера поддерживать на неизменном уровне только линейную скорость переносного вращения, то ускорение Кориолиса будет равно нулю. Возникающее при этом движение по спирали осуществляется только с центростремительным ускорением, что на первый взгляд выглядит парадоксальным. Однако это не равномерное вращательное движение. Его переменное центростремительное ускорение регулируется радиальной силой, периодически изменяющей связь с центром вращения.

При этом геометрический центр кривизны непрерывно изменяет своё положение в пространстве за счёт свободного движения тела по касательной в момент ослабления связи. При этом изменения по направлению радиальной скорости, как такового не происходит. Изменяет направление касательная скорость. А парадоксальность такого псевдо вращательного движения состоит в том, что в классической физике за центростремительное ускорение неоправданно принимается особый вид линейного однородного ускорения вместо разновеликих и разнонаправленных ускорений по изменению направления на самом деле.

В классической физике истинная сила Кориолиса-Кеплера отсутствует. Поэтому в расчёте ускорения Кориолиса она ошибочно исходит из приращения движения, соответствующего полной поддерживающей силе, что приводит к удвоению ускорения Кориолиса. Это требует качественной и соответственно количественной коррекции классической версии явления Кориолиса и анализа причин, по которым классическое дифференцирование не видит этой ошибки.

Начнём с прямолинейного движения, в котором ошибки не столь критичны и ограничиваются лишь некоторым некритичным для истины абстрагированием от реальности. Итак, на рисунке (4.1.1.1) показаны два отдельных участка прямолинейного равноускоренного движения с координатами (18 м, 21 м) и (21м, 26 м) с секундным интервалом внутри каждой пары координат.

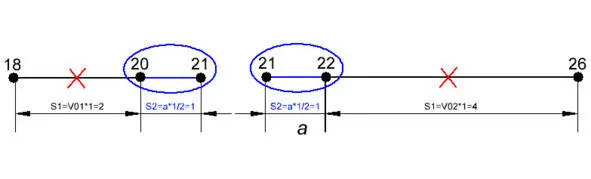
Рис. 4.1.1.1

В физике есть известная всем школьная формула пути для равноускоренного движения (S = V 0+ a * t 2/ 2), из которой следует, что ускорение равно (a = 2 * (S – V 0* t) / t 2). Как видно, пресловутая двойка не является эксклюзивной исключительно только для явления Кориолиса. Она имеет принципиальное значение для определения ускорения через приращение пути любого равноускоренного движения, т.к. средняя скорость, которая и определяет пройденное расстояние, вдвое меньше мгновенной скорости, достигнутой за счёт ускорения за то же самое время. Однако при определении ускорения через дифференцирование координат эту формулу не используют, т.к. для неё недостаточно одних только координат, нужна ещё и начальная скорость.

Если координаты движения можно легко измерить в любой заданной системе отсчёта, то вычленить начальную скорость в составе переменного движения в двух координатах без дополнительных данных не представляется возможным. Поэтому приращение ускоренного движения определяется в классической физике по трёхточечной схеме, как разность средних скоростей двух смежных участков, имеющих три координаты, одна из которых общая. В нашем примере прямолинейного движения это по-прежнему координаты (18 м), (21 м) и (26 м) вдоль заданной оси с секундным интервалом между ними (см. Рис. 4.1.1.2). Но теперь мы их рассмотрим, как смежные участки с учётом общей точки (21 м).

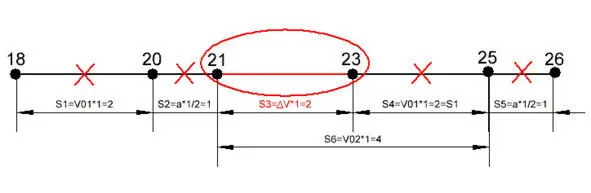
Рис. 4.1.1.2

Как показано на рисунке, при вычитании отрезков (21 – 26) минус (18 – 21) расстояние (S1 и S2), пройденное с начальной скоростью (V 0), а также расстояние, пройденное за счёт ускорения (S2) и (S5) взаимно уничтожаются. Остаётся только отрезок пути (S3 = ∆V * t), где (∆V = Vк – V 01), (Vк) – конечная скорость на участке (18 – 21). Тогда ускорение равно ( a = S3 / t 2). Это соответствует школьной формуле пути при равноускоренном движении только без двойки в знаменателе (S3 = a * t 2). Как видно, на участке (S3) ускорения собственно и нет, т.е. для школьной формулы это академическая абстракция. Очевидно, также, что приращение скорости на смежных участках равно разнице их средних скоростей, что в единичном интервале времени опять же соответствует (S3). Но прирост средней скорости даёт и среднее ускорение при вычислении.

Стопроцентная точность трёхточечной схемы обеспечивается только при равноускоренном движении на всём протяжении обоих смежных участков. В противном случае среднее ускорение в окрестностях граничной точки, которое при тех же самых координатах может отличаться от ускорения равноускоренного движения вдвое. Например, при одних и тех же координатах с нашими данными за исключением нулевого ускорения на втором участке разница средних скоростей (4 – 3 = 1), будет соответствовать вдвое меньшему ускорению (1 / 1 = 1), чем если бы постоянное по величине ускорение (2) было бы на обоих участках (2 / 1 = 1).