Стивен Вайнберг - Пояснюючи світ

Представлені нижче примітки описують наукове та математичне підґрунтя багатьох історичних досягнень, розглянутих у цій книжці. Читачі, які трохи вивчали алгебру та геометрію у школі чи університеті й не зовсім забули те, чого навчилися, не повинні мати якихось проблем із рівнем математики в цих примітках. Але я намагався структурувати цю книжку так, щоб читачі, яких не цікавлять технічні моменти, могли пропустити ці примітки й усе одно зрозуміти основний текст.

Невеличке попередження: описані в цих примітках міркування не обов’язково ідентичні тим, що відповідали конкретним періодам історії. Адже від Фалеса до Ньютона стиль математики, застосовуваний у розв’язанні фізичних проблем, був значно більш геометричний і менш алгебраїчний, ніж сьогодні. Аналізувати ці проблеми в такому геометричному стилі було б складно для мене та нудно для читачів. Тому в цих примітках я продемонструю, як результати, що їх отримували натурфілософи минулого, справді випливають (або у деяких випадках не випливають) зі спостережень та припущень, на які вони спиралися, але без спроб точно відтворити подробиці їхніх міркувань. Примітки

1. Теорема Фалеса

2. Платонові тіла

3. Гармонія

4. Теорема Піфагора

5. Ірраціональні числа

6. Гранична швидкість

7. Краплі, що падають

8. Відбиття

9. Плаваючі й занурені тіла

10. Площі кіл

11. Розміри Сонця й Місяця та відстані до них

12. Розмір Землі

13. Епіцикли для внутрішніх та зовнішніх планет

14. Місячний паралакс

15. Синуси та хорди

16. Горизонти

17. Геометричне доведення теореми про середній градус швидкості

18. Еліпси

19. Елонгації й орбіти внутрішніх планет

20. Добовий паралакс

21. Правило рівних площ та еквант

22. Фокусна відстань

23. Телескопи

24. Гори на Місяці

25. Гравітаційне прискорення

26. Параболічні траєкторії

27. Виведення закону заломлення світла за аналогією з тенісним м’ячиком

28. Виведення закону заломлення світла з принципу найменшого часу

29. Теорія райдуги

30. Виведення закону заломлення світла із хвильової теорії світла

31. Вимірювання швидкості світла

32. Доцентрове прискорення

33. Порівняння Місяця з тілом, що падає

34. Закон збереження імпульсу

35. Маси планет

1. Теорема Фалеса

Теорема Фалеса використовує просте геометричне міркування, щоб отримати неочевидний висновок про властивості кіл та трикутників. Хай хто, Фалес чи хтось інший, першим довів цю теорему, її буде корисно розглянути як приклад того, що давні греки знали про геометрію до часів Евкліда.

Уявіть собі коло з будь-яким діаметром. Нехай А і B будуть точками, де цей діаметр перетинає коло. Проведемо лінії від А і B до будь-якої іншої точки P на колі. Діаметр та відрізки АР і ВР утворюють трикутник ABP . Теорема Фалеса говорить, що такий трикутник прямокутний: кут трикутника ABP у точці P прямий, тобто дорівнює 90°.

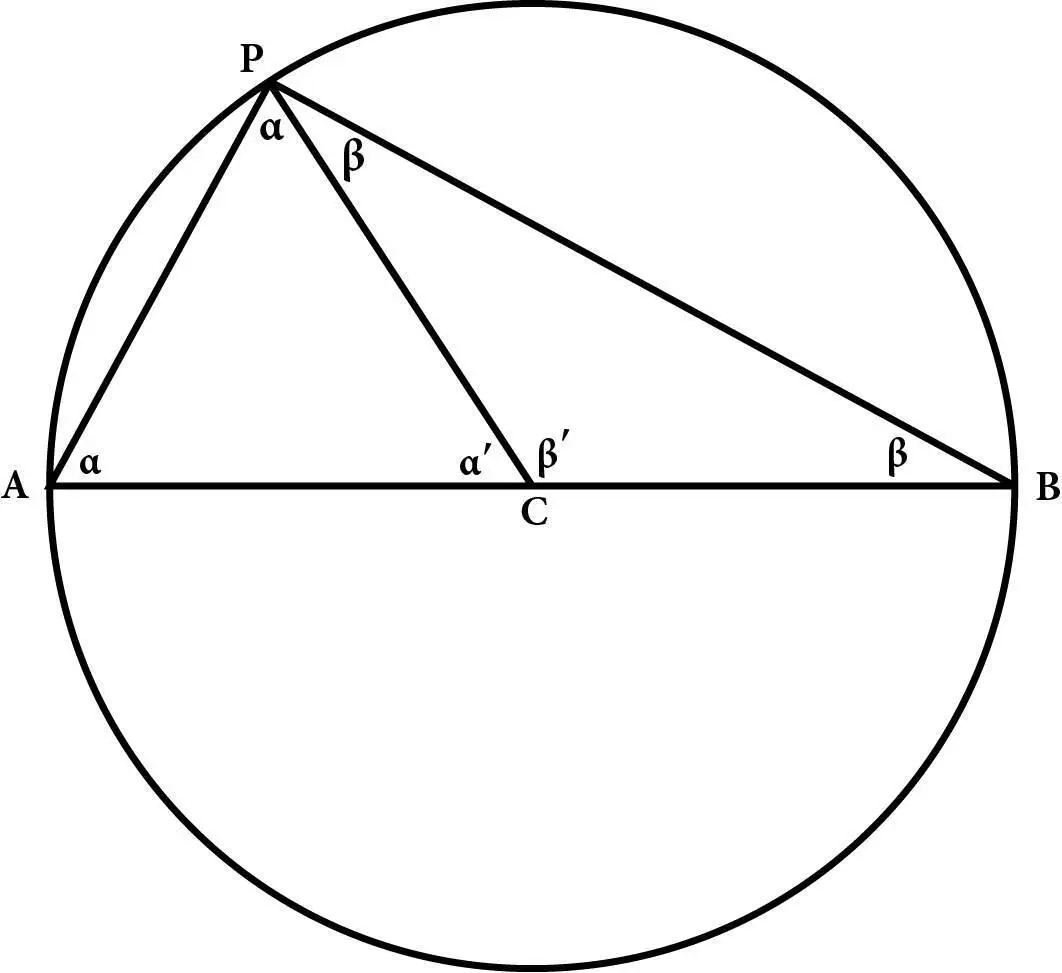
Рис. 1.Доведення теореми Фалеса. Ця теорема стверджує: де б точка P не була розташована на колі, кут між відрізками від кінців діаметра до P буде прямий.

Хитрість у доведенні цієї теореми полягає в тому, щоб з’єднати відрізком центр кола C з точкою P . Цей відрізок ділить трикутник ABP на два трикутники: ACP та BCP (див. рис. 1). Обидва ці трикутники рівнобедрені, тобто трикутники з двома рівними сторонами. У трикутнику ACP сторони CА та CP – це радіуси кола, які, за визначенням кола, мають однакову довжину (ми позначаємо сторони трикутника за кутовими точками, які вони з’єднують). Так само у трикутнику BCP сторони CB та CP також рівні. У рівнобедреному трикутнику кути, що прилягають до двох рівних сторін, рівні, тому кут α (альфа) в місці перетину сторін AP та AC дорівнює куту в місці перетину сторін AP та CP , а кут β (бета) в місці перетину сторін BP та ВС дорівнює куту в місці перетину сторін BP та CP . Сума кутів будь-якого трикутника дорівнює двом прямим кутам [68], або, у більш знайомих нам термінах, 180°, тож якщо ми позначимо третій кут трикутника ACP (кут у місці перетину сторін AC та CP ) як αʹ і так само кут у місці перетину сторін ВС та CP позначимо як βʹ, то отримаємо такі рівності:

2α + αʹ = 180° і 2β + βʹ = 180°.

Додавши ці два рівняння й переставивши доданки, отримаємо таке: