Йэн Стюарт - Математика космоса [Как современная наука расшифровывает Вселенную]

Поверхность футбольного мяча — это двумерное многообразие. Пуанкаре был пионером алгебраической топологии, особенно трехмерной, и однажды он обнаружил, что ошибся. Чтобы доказать это (в отличие от политиков, математики делают подобные вещи), он придумал аналогичное трехмерное многообразие. Пуанкаре построил его, склеив вместе два тора, но позже было найдено более элегантное решение с использованием додекаэдра. Речь шла о хитроумном варианте плоского трехмерного тора, который изготавливается посредством концептуального склеивания (отождествления) противоположных граней куба. Если проделать то же самое с додекаэдром и к тому же перед склеиванием повернуть каждую грань, то получится трехмерное многообразие — додекаэдрическое пространство. Подобно плоскому 3-тору, оно не имеет границы: все, что проходит внутрь сквозь грань, тут же появляется из противоположной грани. Оно имеет положительную кривизну и конечный размер.

Уикс проработал статистические характеристики флуктуаций реликтового излучения для случая, когда Вселенная представляет собой додекаэдрическое пространство, и обнаружил прекрасное совпадение с данными WMAP. Группа ученых под руководством Жана-Пьера Люмине пришла к выводу, что Вселенная такой формы должна иметь размер около 30 миллиардов световых лет в поперечнике — совсем неплохо. Однако недавние наблюдения, похоже, опровергают эту теорию, внушая разочарование всем поклонникам Платона на планете.

Трудно понять, каким образом мы могли бы доказать бесконечность Вселенной, но если она конечна, не исключено, что мы сможем установить ее форму. В конечной Вселенной [78] Здесь надо различать понятия бесконечности и безграничности. Рассматриваемые модели Вселенной, даже конечные по объему или массе, не имеют пространственных границ, то есть безграничны. — Прим. ред. должно существовать некоторое количество замкнутых геодезических кривых — кратчайших путей, образующих петли, как образует петлю резинка, надетая на скатанную газету. Световой луч, движущийся вдоль такой геодезической кривой, рано или поздно вернется в начальную точку. Направьте туда мощный телескоп — и вы увидите собственный затылок. Только учтите, на это может понадобиться некоторое время — ровно столько, сколько требуется свету, чтобы обойти всю Вселенную, так что вам нужно будет постоять спокойно и запастись терпением. Кроме того, ваш затылок, когда вы его увидите, может оказаться перевернут вниз головой или зеркально отражен по отношению к оригиналу.

Серьезный математический анализ, учитывающий конечность скорости света, предсказывает, что в таких обстоятельствах в реликтовом излучении должны наблюдаться повторяющиеся закономерности, когда одни и те же флуктуации располагаются на небе вполне различимыми кругами. Это происходит потому, что фотоны реликтового излучения, доходящие до Земли сегодня, начинали свой путь примерно с одинаковых расстояний — они имеют начало на сфере, на «поверхности последнего рассеяния». Если Вселенная конечна, а эта сфера больше, чем Вселенная, то она сворачивается и пересекается сама с собой. Пересечением двух сфер является окружность, и каждая точка на такой окружности благодаря свертыванию посылает микроволны к Земле в двух разных направлениях.

Мы можем проиллюстрировать этот эффект для двумерного аналога, где геометрия проще. Если квадрат на рисунке достаточно велик, чтобы содержать круг, никакого пересечения за счет свертывания не возникает. Если же квадрат достаточно мал, чтобы круг обернулся дважды, геометрия пересечений окажется более сложной.

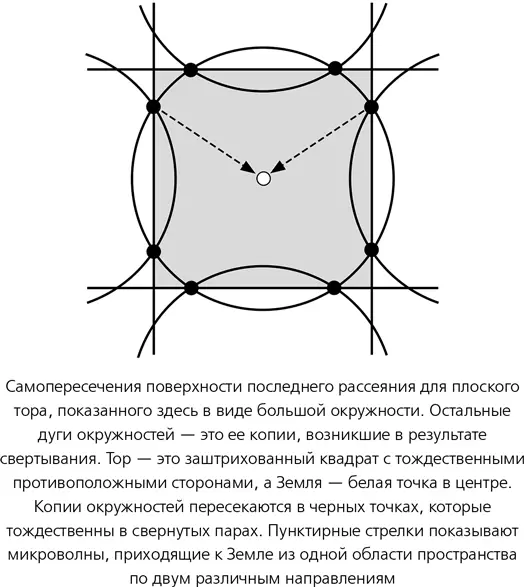
Для плоского трехмерного тора квадрат следует заменить на куб, окружности — на сферы, а точки превратятся в окружности на гранях куба, которые опять же следует отождествить попарно. Пунктирные линии становятся конусами. С Земли (в этом случае) мы наблюдаем в небе пару особых окружностей, которые на самом деле представляют собой одну и ту же отдаленную окружность, видимую с двух этих направлений. Флуктуации реликтового излучения около этих двух окружностей должны быть почти идентичными, и это можно обнаружить при помощи статистических корреляций флуктуаций температуры фона: мы ожидаем увидеть одинаковую последовательность горячих и холодных участков вдоль каждой окружности, где «горячий» и «холодный» означают чуть более высокую или низкую температуру по сравнению со средней.