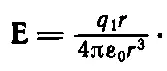 (12.4)
(12.4)
А затем мы пишем
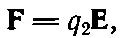 (12.5)
(12.5)
т. е. связываем силу, поле и заряд в поле. В чем же суть всего этого? Суть в том, что анализ разделяется на две части. Одна часть говорит, что что-то создает поле, а другая — что оно действует на что-то. Позволяя нам рассматривать две части независимо, это разделение упрощает во многих случаях расчеты трудных задач. Когда зарядов много, то сперва мы рассчитываем суммарное электрическое поле, создаваемое этими зарядами в R , а потом, зная величину заряда, помещенного в R , находим силу, действующую на него.
Да и в случае тяготения мы можем сделать то же самое. Сила теперь F=- Gm 1 m z r/ r 3. Анализ полностью совпадает: сила притяжения тела в поле тяготения равна произведению массы тела на поле С. Сила, действующая на m 2, равна массе m 2, умноженной на поле С, созданное массой m 1, т. е. F= m 2 G . Значит, поле С, создаваемое массой m 1, есть С=- Gm 1 r/ r 3; оно, как и электрическое поле, направлено по радиусу.
Такое разделение на две части не так уж тривиально, как могло бы показаться на первый взгляд. Оно было бы тривиальным, было бы просто иной записью того же самого, если бы законы действия сил были совсем просты, но они очень сложны, и оказывается, что поле настолько реально, что почти не зависит от объектов, создающих его. Можно колебать заряд, и влияние этого (поле) скажется на расстоянии. Если колебания прекратятся, в поле все равно будут ощущаться следы этих колебаний, потому что взаимодействие двух частиц не происходит мгновенно. Оттого и желательно уметь запоминать, что здесь раньше происходило. Если сила действия на заряд зависит от того, где другой заряд был вчера и каким он тогда был, то должна быть возможность проследить за тем, что было вчера; в этом и состоит сущность поля. Чем сложнее силы, тем реальней поле, и наша техника разделения становится все менее и менее искусственной.
Желая анализировать силы при помощи полей, мы нуждаемся в законах двоякого рода. Первые — это отклик на поле. Они дают нам уравнения движения. Например, закон отклика массы на поле тяжести состоит в том, что сила равна массе, умноженной на поле тяжести, или если тело еще и заряжено, то отклик заряда на электрическое поле равен заряду, умноженному на электрическое поле. Вторая часть анализа природы в таких положениях — это формулировка законов, определяющих напряженность поля и способ его возникновения. Эти законы иногда называют уравнениями поля . В нужный момент мы с ними познакомимся, а пока скажем о них лишь несколько слов.
Вот вам для начала самое замечательное свойство поля, оно абсолютно точно и легко усваивается. Общее электрическое поле, создаваемое группой источников, есть векторная сумма полей, создаваемых по отдельности первым, вторым и т. д. источниками. Иными словами, когда поле создано множеством зарядов и если отдельное поле первого есть Е 1, а второго — Е 2 и т. д., то мы должны просто сложить эти векторы, чтобы получить общее поле. Принцип этот выражается в виде
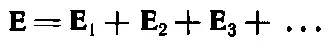 (12.6)
(12.6)
или, в согласии с определением поля,
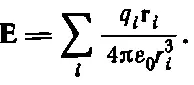 (12.7)
(12.7)
Можно ли эти методы применить к тяготению? Силу притяжения двух масс m 1и m 2Ньютон выразил в виде F=- Gm 1 m 2 r / r 3. Но в соответствии с понятием поля можно сказать, что m 1создает поле Сво всем окружающем пространстве и сила, притягивающая m 2, равна
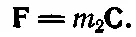 (12.8)
(12.8)
По аналогии с электричеством
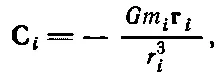 (12.9)
(12.9)
и тогда поле тяжести нескольких масс равно
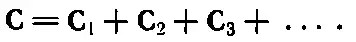 (12.10)
(12.10)
В гл. 7, где рассматривалось движение планет, мы по существу использовали именно этот принцип. Мы складывали все векторы сил, чтобы обнаружить общую силу, действующую на планету. Разделив на ее массу, мы и получим (12.10).
Читать дальше

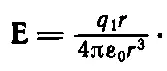 (12.4)
(12.4)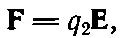 (12.5)
(12.5)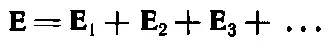 (12.6)
(12.6)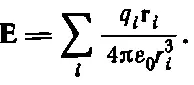 (12.7)
(12.7)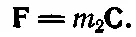 (12.8)
(12.8)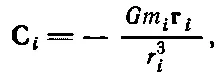 (12.9)
(12.9)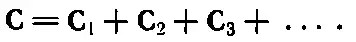 (12.10)
(12.10)




