§ 4. Фундаментальные силы. Поля
Мы хотим побеседовать теперь об оставшихся фундаментальных силах. Называем мы их фундаментальными потому, что законы их действия фундаментально просты. Сперва рассмотрим электрическую силу.
Тела несут в себе электрические заряды, которые состоят просто из электронов и протонов. Если два тела заряжены, меж ними действует электрическая сила; если величины зарядов равны соответственно q 1и q 2, то сила изменяется обратно пропорционально квадрату расстояния между зарядами
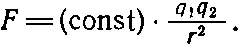
Для разноименных зарядов этот закон похож на закон тяготения, но для одноименных сила становится отталкивающей и ее знак (направление) меняется. Сами заряды q 1и q 2могут быть и положительными и отрицательными; практически, пользуясь формулой, можно получить правильный знак силы, если поставить возле q их знаки. Сила направлена вдоль отрезка, соединяющего заряды. Коэффициент в формуле зависит, конечно, от выбора единиц силы, заряда и длины. Обычно заряд измеряют в кулонах , промежуток — в метрах , а силу — в ньютонах . Чтобы получить силу в ньютонах, константа (по историческим причинам ее пишут в виде 1/4πε 0) должна принимать численное значение
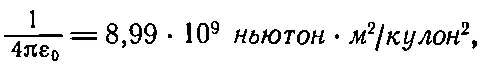 (а)
(а)
т. е.
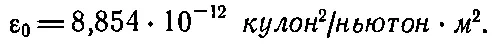 (б)
(б)
Итак, закон силы для покоящихся зарядов имеет вид
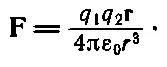 (12.2)
(12.2)
В природе самый важный из всех зарядов — это заряд отдельного электрона, он равен 1,60·10 -19 кулон . Кто работает не с большими зарядами, а с электрическими силами между фундаментальными частицами, те предпочитают как-то выделить сочетание (q эл) 2/4πε 0, в котором q элопределяется как заряд электрона. Это сочетание часто встречается, и для упрощения расчетов его обозначают ε 2; его численное значение в системе СИ оказывается равным (1,52·10 -14) 2. Удобство пользования константой в этой форме заключается в том, что сила в ньютонах , действующая между двумя электронами, запишется просто как ε 2/r 2(r дано в метрах ), без каких-либо коэффициентов. На самом деле электрические силы намного сложней, чем следует из этой формулы, потому что формула относится к покоящимся телам. Сейчас мы рассмотрим более общий случай.
Анализ фундаментальных сил (не сил трения, а электрических сил или сил тяготения) связан с интересным и очень важным понятием.
Теория этих сил намного сложнее, чем об этом следует из закона обратных квадратов. Закон этот действует лишь тогда, когда взаимодействующие тела находятся в покое. Поэтому нужен усовершенствованный метод обращения с очень сложными силами — силами, которые возникают, когда тела начинают двигаться запутанным образом. Как оказалось, для анализа сил такого типа очень полезен подход, основанный на введении понятия «поля». Чтобы пояснить мысль на примере, скажем, электрической силы, положим, что в точке Р находится заряд q 1, а в точке R — заряд q 2. Сила, действующая между зарядами, равна
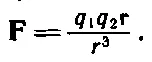 (12.3)
(12.3)
Чтобы проанализировать эту силу при помощи понятия поля, мы говорим, что заряд q 1в точке Р создает в точке R такие «условия», при которых заряд q 2, попадая в R , «ощущает» действие силы. Это один из мыслимых путей описания действия силы. Может быть, он выглядит странно: мы говорим, что действие силы Fна заряд q 2в точке R можно разбить на две части — на q 2и Е, причем величина Есуществует в точке R безотносительно к тому, есть ли там заряд или нет (лишь бы все прочие заряды были на своих местах). Величина Еесть «условие», созданное зарядом q 1, а F— ответ, отклик заряда q 2на Е. Величину Еназывают электрическим полем . Это — вектор. Формула для электрического поля Е, созданного в точке R зарядом q 1находящимся в точке Р , такова: заряд q 1, умноженный на постоянную 1/4πε 0, деленный на r 2(r — расстояние от Р до R ); поле действует по направлению радиус-вектора (вектор направления радиус-вектора — это радиус-вектор, деленный на свою длину). Таким образом, выражение для Етаково:
Читать дальше

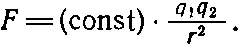
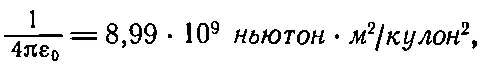 (а)
(а)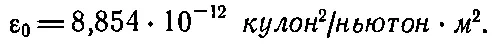 (б)
(б)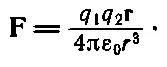 (12.2)
(12.2)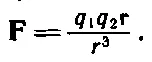 (12.3)
(12.3)




