Ричард Фейнман - Том 1. Механика, излучение и теплота

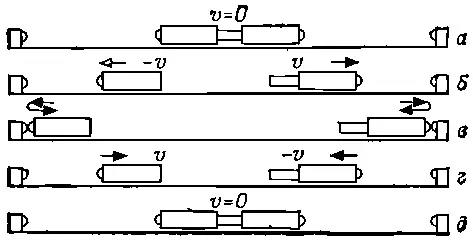
Фиг. 10.3. Схема эксперимента с равными массами.

Это интересный опыт. И в действительности происходит все так, как мы рассказали.

Теперь на очереди проблема посложнее. Допустим, мы имеем две массы, причем одна движется со скоростью v , а другая стоит на месте. Затем первая ударяет по второй и они слипаются. Что произойдет дальше? Образуется одно тело с массой 2m, которое как-то будет двигаться. Но с какой скоростью? Вот в чем вопрос. Чтобы ответить на него, предположим, что мы едем вдоль желоба на автомобиле. Все законы физики должны при этом выглядеть точно так же, как и прежде, когда мы стояли на месте. Мы начали с того, что если столкнуть два тела с равными массами и одинаковыми скоростями v , то после слипания они останавливаются. А теперь представьте, что в это время мы катим на автомобиле со скоростью — v . Какую же картину мы увидим? Ясно, что одно из тел, поскольку оно все время летит рядом с автомобилем, будет казаться нам неподвижным. Второе же, которое движется навстречу со скоростью v , покажется нам несущимся с удвоенной скоростью 2 v (фиг. 10.4).

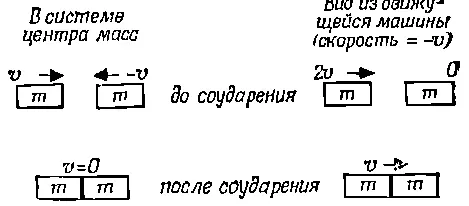
Фиг. 10.4. Неупругое соударение равных масс.

Наконец, образовавшееся после соударения и слипания тело будет казаться нам летящим со скоростью v . Отсюда мы делаем вывод, что если тело, летящее со скоростью 2 v , ударяется о покоящееся тело той же массы и прилипает к нему, то образовавшееся тело будет двигаться со скоростью v , или (что математически то же самое) тело со скоростью v , ударяясь о покоящееся тело той же массы и прилипая к нему, образует тело, движущееся со скоростью v /2. Заметьте, что если умножить массы тел на их скорости и сложить их, то получим одинаковый результат как до столкновения ( mv +0), так и после (2 m · v /2). Вот как обстоит дело, если тело, обладающее скоростью v , столкнется с телом, находящимся в покое.

Точно таким же образом можно определить, что произойдет, когда сталкиваются два одинаковых тела, каждое из которых движется с произвольной скоростью.

Пусть одно тело летит со скоростью v 1, а другое — со скоростью v 2в том же направлении ( v 1> v 2). Какова будет их скорость после соударения? Давайте снова сядем в машину и поедем, скажем, со скоростью v 2. Тогда одно из тел будет казаться нам стоящим на месте, а второе — налетающим на него со скоростью v 1- v 2. Эта ситуация уже знакома нам, и мы знаем, что после соударения скорость нового тела по отношению к машине будет равна 1/ 2( v 1- v 2). Что же касается действительной скорости относительно земли, то ее можно найти, прибавив скорость автомобиля: v = 1/ 2( v 1- v 2)+ v 2или 1/ 2( v 1+ v 2) (фиг. 10.5).

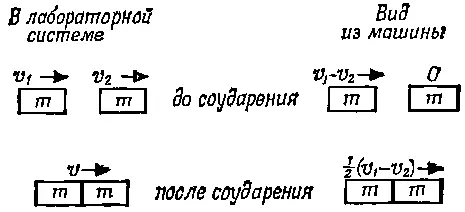
Фиг. 10.5. Другой случай неупругого соударения равных масс.

Обратите внимание, что снова

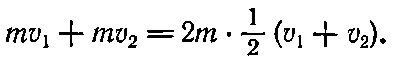(10.6)

Таким образом, принцип относительности Галилея помогает нам разобраться в любом соударении равных масс. До сих пор мы рассматривали движение в одном измерении, однако на основе его становится ясным многое из того, что будет происходить в более сложных случаях соударения: нужно только пустить автомобиль не вдоль направления движения тел, а под каким-то углом. Принцип остается тем же самым, хотя детали несколько усложняются.

Чтобы экспериментально проверить, действительно ли тело, летящее со скоростью v после столкновения с покоящимся телом той же массы, образует новое тело, летящее со скоростью v /2, проделаем на нашей замечательной установке следующий опыт. Поместим в желоб три тела с одинаковыми массами, два из которых соединены цилиндром со взрывателем, а третье находится вблизи одного из них, хотя и несколько отделено от него. Оно снабжено клейким амортизатором, так что прилипает к тому телу, которое ударяет его. В первое мгновение после взрыва мы имеем два объекта с массами m, движущимися со скоростью v каждое. В последующее мгновение одно из тел сталкивается с третьим и образует новое тело с массой 2 m , которое, как мы полагаем, должно двигаться со скоростью v /2. Но как проверить, что скорость его действительно v /2? Для этого мы вначале установим тела таким образом, чтобы расстояния до концов желоба относились как 2:1, так что первое тело, которое продолжает двигаться со скоростью v, должно пролететь за тот же промежуток времени вдвое большее расстояние, чем скрепившиеся два других тела (с учетом, конечно, того малого расстояния Δ, которое второе тело прошло до столкновения с третьим). Если мы правы, то массы m и 2m должны достичь концов желоба одновременно; так оно и происходит на самом деле (фиг. 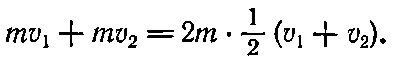10.6).